АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Определить, сколько килограммов корма каждого вида надо взять для составления суточного рациона, чтобы он был достаточно питательным и имел наименьшую себестоимость

Читайте также:
  1. S: На пути световой волны, идущей в воздухе, поставили стеклянную пластинку толщиной 1 мм. На сколько изменится оптическая длина пути, если волна падает на пластинку нормально?
  2. S: Определить длину отрезка, на котором укладывается столько же длин волн в вакууме, сколько их укладывается на отрезке 3 мм в воде.
  3. V. СКОЛЬКО ОТЦОВ БЫЛО У РОБЕРТА?
  4. А затем дважды в неделю в течение 2 мес.) является достаточно эффективной дополнительной терапией в
  5. А может взять и все отобрать
  6. А не о том, чтобы красиво войти.
  7. А Христос за всех умер, чтобы живущие уже не для себя жили, но для умершего за них и воскресшего.
  8. Алгоритм составления уравнения химической реакции
  9. Алекс сидел за барабанами и, загороженный справа колонкой, смотрел, чтобы с Элис ничего не случилось.
  10. Анализ взаимосвязи между обобщающими, частными показателями экономической эффективности деятельности предприятия и эффективностью каждого научно-технического мероприятия
  11. Апрель 2011. За несколько дней до знакомства с Скарлетт. Взято из воспоминаний Найла и Гарри.
  12. Артериальная недостаточность

Обозначим через суточный рацион, в котором – количество корма вида I (в кг); – количество корма вида II. Очевидно, . В рационе вещества А будет содержаться ед. Но оно должно входить в рацион в количестве не менее 1000 ед., значит . Аналогичным образом получим еще два неравенства, связанных с минимальной потребностью в питательных веществах В и С: . Кроме того, на один рацион нельзя расходовать больше 25 кг корма I и 20 кг корма II, поэтому .

 

Итак, получим общую задачу ЛП:

В сформулированной задаче – себестоимость рациона. От общей задачи ЛП перейдем к основной, введя добавочные переменные:

(А)

 

Применив метод искусственного базиса, запишем вспомогательную задачу:

 

 

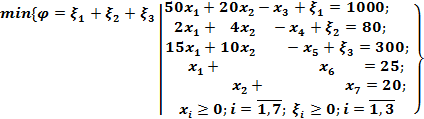
Базис:

Однако можно сократить количество фиктивных переменных, проделав некоторые тождественные преобразования системы (А). Для этого из первого уравнения (1) вычитаем второе (2) и третье (3). Получим систему уравнений, равносильную исходной:

Составим вновь вспомогательную задачу:

 

Базис: Задача почти каноническая.

Исходная таблица

 

                     
B Коэффициенты при неизвестных  
       
       
       
           
           
           

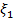
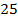
Итерация 1

                     
B Коэффициенты при неизвестных  
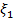
  10/3 -25/24      
1/3        
  -5/3 -35/48      
  -1/3 1/48 -1/48      
             
  10/3 -25/24        
                           

 

Итерация 2

B Коэффициенты при неизвестных  
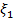
    -5/16       3/10
        -1/10
    -5/4     1/2
    1/40 -1/8     1/10
    -1/80 5/16     -3/10
              -1
                     

Следовательно, линейная система (А) обладает планами. Выпишем каноническую систему , равносильную исходной, из последней симплексной таблицы вспомогательной задачи ЛП:

;

(*)

.

xi 0, I =1,7

Далее решаем почти каноническую задачу: при условиях (*).

Исходная таблица

                   
B Коэффициенты при неизвестных
 
    -5/16        
         
    -5/4      
    1/40 -1/8      
    -1/80 5/16      
    - -7/16        

 

Получено оптимальное решение ( =15, = 25/2, = 0, = 0, = 50, = 10, 15/2), . (см.А).

Вывод: для составления суточного рациона надо взять 15 кг корма вида I и 12.5 кг корма вида II. Рацион будет достаточно питательным, его себестоимость минимальна, а стоимость = 97.5 . Значения добавочных переменных () показывают, что питательных веществ видов А и В в рационе содержится соответственно 1000 и 80 ед., а веществ вида С на 50 ед. больше минимальной нормы – 300 ед. Кроме того, для суточного рациона будет израсходовано корма вида I на 10 кг меньше, имеющегося в запасе, а корма вида II – на 7.5 кг меньше.

В заключение отметим, что для некоторых типов задач ЛП (например, для транспортных задач) разработаны дополнительно специальные методы решения, оказывающиеся в ряде случаев более удобными и экономными.

 

Примечание: Если среди базисных переменных завершающей симплексной таблицы вспомогательной задачи содержится хотя бы одно искусственное переменное, то необходимо провести дополнительные преобразования, прежде чем придем к базису без искусственных переменных [4, c. 44].

Пусть, например, в завершающей симплексной таблице вспомогательной задачи остались ζ1, ζ2, Х1. Выпишем систему, которая при ζ1 = ζ2 = ζ3 = 0 будет неканонической

 



 

Если , то делим 2-е уравнение на , затем исключим из 1-го и 3-го уравнений (точно также, как в методе Гаусса). Получим

 

 

Затем исключим аналогично из 1-го и 2-го уравнения. Придем к канонической системе, равносильной исходной.

Глава 3. Целочисленное линейное программирование.

 

Важное значение в ЛП имеет случай, когда неизвестные целочисленные. Задача ЛП с дополнительным условием целочисленности неизвестных исследуется в новой области математического программирования – целочисленном (дискретном) программировании (ЛЦП).


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.008 сек.)