 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
При условиях
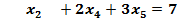
По теореме Кронекера-Капелли [2] для совместности линейной системы необходимо и достаточно, чтобы ранг матрицы A r(A) был равен рангу расширенной матрицы R r(R). r(A) есть наибольший из порядков миноров, отличных от нуля (т.е. r(A) – целое число). Известно, что r(A) не меняется, если к какому-либо столбцу (строке) прибавить произвольную линейную комбинацию других столбцов (строк) этой
матрицы. Кроме того, r(A) не изменится, если какой-либо столбец, состоящий из нулей, удалить. Итак
=?
Прибавив первый столбец, умноженный на (-1), к пятому, а затем и к четвертому, получим
Выполняем аналогичные преобразования и, в итоге, получим
Соответственно, ранг расширенной матрицы будет равен также
= 3.
Следовательно, наша система совместна.
При формулировке задач ЛП могут быть два случая:
1. 
(
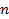– количество неизвестных в системе).
Решение системы единственное. Задача ЛП не имеет смысла.
2. 
. Этот случай представляет для нас интерес. Неизвестных больше, чем уравнений в системе. Задаваясь каждый раз 
свободными неизвестными, получим в итоге множество решений системы, из которых в соответствии с функцией цели выбирается то решение, которое дает оптимальный результат. В нашем примере 
Как было показано выше, в исходном числовом примере система уравнений каноническая, задача - каноническая.
Итак,
при условиях
В системе базисных переменных три 
, а свободных два 
. Выразим целевую функцию и базисные переменные через свободные переменные 
.
Но F уже выражена, а базисные переменные примут следующий вид:
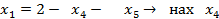
(2)
(3)
Все 
должны быть неотрицательны, т.е.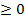 
.
Зададим наименьшие возможные значения 
, при этом получим 
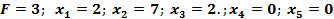. Это решение, удовлетворяющее ограничениям, т.е. допустимое. Проанализируем, нельзя ли увеличением значений 
уменьшить 
? Из выражения
следует, что при увеличении 
возрастает. При 
будет отрицательным 
самый ненадёжный из 
, Значит, следует принять 
. Тогда получим новый допустимый план: 
При этом 
Переменное 
выведено из базиса, вместо него в базис включен 
а 
стали свободными переменными. Выразим новые базисные переменные 
и функцию F через 
. 
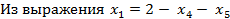найдём 
. Подставим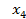 
в выражения
(1), (2), (3). Получим:
Из выражения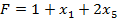 
следует, что должны быть равны нулю, так как в противном случае F будет расти.
Достигнуто оптимальное решение: 
Полученное решение называется базисным, так как свободные переменные равны нулю. Следует отметить, что оптимальное решение получено, когда в выражении для F полученные значения коэффициентов при неизвестных положительны, а в процессе решения значение F только понижалось от 3 до 1, т.е. перебор был организованным.
Поиск по сайту: