Пример. Исследовать характер точек перегиба функции f (х) = х3 - 2х2 + х + 1:

Исследовать характер точек перегиба функции f (х) = х³ - 2х² + х + 1:

Решение. 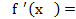Зх² - 4х+1 = 0, тогда (Зх - 1)(х - 1) = 0, т. е. х = 1/3 или х = 1.

При х = 1/3 производная 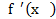меняет знак с положительного на отрицательный, а при

х = 1 - с отрицательного на положительный. Следовательно, в точке х = 1/3 дости­гается максимум, а в точке х = 1 - минимум. Этот пример может быть решен более простым способом, если вычислить вторую производную f''' = 6х — 4: f'''1/3) = -2, т. е. отрицательна, и при х = 1/3 достигается максимум; f''' (1) = 2, т. е. положительна, и при х = 1 достигается минимум. Неоднозначность, возникающую при f''' (*) = 0, можно разрешить, увели­чив количество членов в формуле разложения в ряд Тейлора

:

+ ) +

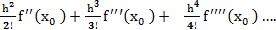
При этом можно сформулировать следующее правило: Если функция f (х) и ее производные непрерывны, то точка х₀ является точкой экстремума (максимума или минимума) тогда, и только тогда, когда п четное, где n — порядок первой необращающейся в нуль в точке х₀ производной.

Если 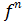< 0, то в точке х₀ достигается максимум,

если > 0, то в точке х₀ достигается минимум.

2). Функция у = f () (нескольких переменных).

Необходимое условие экстремума. Если х*() - точка локального безусловного экстремума непрерывно дифференцируемой в точке х* функции

у = f (), то все её частные производные первого порядка в этой точке равны нулю, то есть

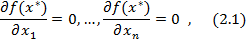
или в векторной форме 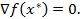Точки, удовлетворяющие условию (2.1), называются стационарными.

Достаточное условие экстремума. Если в стационарной точке х* функция f(x) дважды дифференцируема и матрица её вторых производных Н(х*) (матрица Гессе) положительно определена (то есть все её главные миноры 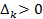), то есть 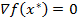и Н(х*) > 0, то х*- точка локального минимума.(Напомним, что для прямоугольной матрицы А_mn определитель квадратной матрицы К-го порядка называется минором К-го порядка матрицы А_mn)

Матрица Гессе имеет вид:

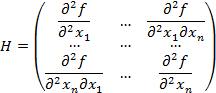
Пример. Исследовать на экстремум функцию

.

Решение. Запишем необходимые условия экстремума:

Проверим достаточные условия. Матрица Гессе имеет вид:

,

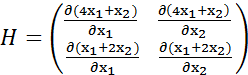то есть 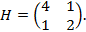Так как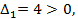 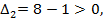то H(x*)>0 и точка x*=(0,0) является точкой локального минимума.

Для того чтобы найти, является ли данная квадратичная форма положительно определенной, мож­но воспользоваться теоремой, которая формулируется следующим образом. Для положительной определенности квадратичной фор­мы необходимо и достаточно, чтобы были выполнены условия Сильвестра:

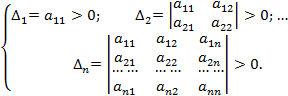
Случай двух переменных. Достаточным условием минимума является по­ложительность главных миноров первого и второго порядков.

Случай трех переменных .Достаточным условием минимума для функции трех переменных является положительность всех трех миноров