Графический способ решения задач линейного программирования и геометрическая интерпретация

Дана задача линейного программирования:

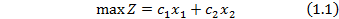
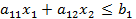
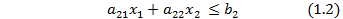
или в краткой форме:

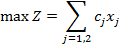
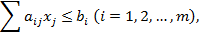
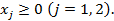
Среди допустимых решений системы (1.2) найти то, которое обращает в максимум линейную форму (1.1).

Уравнение

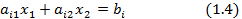
на плоскости х₁Ох₂ определяет прямую, разбивающую всю плоскость на две полуплоскости, каждая из которых лежит по одну сторону от прямой. Прямая (1.4) называется граничной и принадлежит обеим полуплоскостям.

Координаты точек, лежащих в одной полуплоскости, удовлетворяют неравенству
,

а координаты точек, лежащих в другой полуплоскости, удовлетворяют неравенству

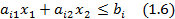
Следовательно, системе неравенств (1.2) удовлетворяет множество точек Х (х₁, х₂ ), лежащих в пересечении полуплоскостей, заданных неравенствами системы.

Пересечение конечного числа полуплоскостей есть некоторая выпуклая многоугольная область Ω, которая называется областью решения системы (1.2). Если система (1.2) противоречива, область Ω пуста. Поставленную задачу (1.1) - (1.3) можно теперь сформулировать следующим образом: среди всех точек многоугольной области Ω найти ту, которая обращает в максимум линейную форму

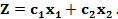
Выбрав произвольное с ₀, запишем уравнение прямой из семейства параллельных прямых, нормальных вектору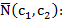

Координаты точки, обращающей в максимум линейную форму (1.1), определяют решение задачи. Линейная форма задачи программирования достигает экстремума в крайней точке выпуклой области Ω. Если линейная форма принимает экстремальное значение более чем в одной крайней точке, она достигает того же значения в любой другой точке, являющейся выпуклой линейной комбинацией этих точек. Искомая точка определяется параллельным перемещением прямой

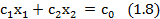
в положительном направлении вектора .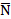

Очевидно, решением задачи на максимум линейной формы является наиболее удаленная крайняя точка, в которой прямая (1.8) встречается с областью Ω. Если же задача линейного программирования сформулирована на минимум линейной формы, то решением задачи будет первая точка, в которой прямая

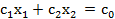
встречается с областью Ω при параллельном перемещении в направлении вектора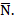

Аналогично геометрически интерпретируется задача линейного программирования и в n -мерном пространстве

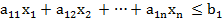
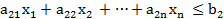
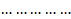
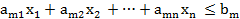
Каждое неравенство a_i1x₁+a_i2x₂+…+a_inx_n ≤ b_i определяет в n-мерном пространстве полупространство, состоящее из точек X(x₁, x₂, …x_n), расположенных по одну сторону от граничной гиперплоскости a_i1x₁+a_i2x₂+…+a_inx_n ≤ b_i и на самой этой гиперплоскости. Пересечение конечного числа полупространств есть выпуклая многогранная область Ω, которая является множеством всех решений системы ограничений записанной задачи.

Значение линейной формы в точке Х' (x'₁, x'₂, …, x'_n) можно рассматривать как уклонение точки Х'(x'₁, x'₂, …, x'_n) от гиперплоскости

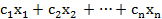= 0,

где под уклонением данной точки от гиперплоскости следует понимать число, полученное в результате подстановки в левую часть уравнения (1.9) вместо x₁, x₂, …, x_n координат точки Х'. Геометрическая интерпретация задачи линейного программирования заключается в отыскании на множестве решений Ω* такой крайней точки, которая наименее (наиболее) уклонена от гиперплоскости (1.9).

Поиск по сайту: