АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Рассмотренные задачи (1) и (2) образуют пару т.н. симметричных двойственных задач

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I-III – зародышевые бугры, из которых образуются различные отделы лица.
  3. I. 1.1. Пример разработки модели задачи технического контроля
  4. I. 1.2. Общая постановка задачи линейного программирования
  5. I. 2.1. Графический метод решения задачи ЛП
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  8. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  9. I. Ситуационные задачи и тестовые задания.
  10. I. Цель и задачи дисциплины
  11. I.5.3. Подготовка данных для задачи линейного программирования
  12. I.5.4. Решение задачи линейного программирования

В общем виде:

 

Задача I Задача II
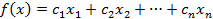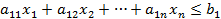
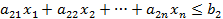
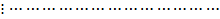
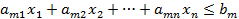
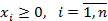
Максимизировать при условиях: Минимизировать 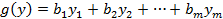при условиях:

 

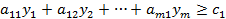
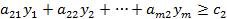
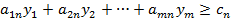
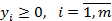
Матрица А здесь транспонируется. Задача II является двойственной к задаче I, а задача I двойственной к задаче II. Обе задачи I и II образуют пару симметричных двойственных задач.

Итак, экономически [4, с.58] I задача трактуется как задача определения оптимального плана выпуска продукции «n» наименований из «m» ресурсов (плана с наибольшей возможной выручкой). Двойственную к I – IIю задачу трактуем как задачу определения оптимальных оценок ресурсов, таких цен единицы каждого ресурса, при которых выручка не превосходила бы затрат на ресурсы и вместе с тем суммарная стоимость ресурсов была бы минимальной.

Теорема: 1. Значение целевой функции задачи I не превосходит значения целевой функции задачи II для любого её плана, т.е. 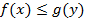(см. пример на использование сырья – текущие значения целевых функций).

Теорема 2. (критерий оптимальности двойственных задач). Если для некоторых планов соответствующих двойственных задач значения целевых функций равны, то эти планы оптимальны.

Основная теорема двойственности. Если одна из двойственных задач I или II имеет решение, то имеет решение и другая, причем значения целевых функций для оптимальных планов обеих задач совпадают.

Теорема: Для того, чтобы задачи максимизации (минимизации) имели решение, необходимо и достаточно, чтобы целевая функция этой задачи была ограничена сверху (снизу) на непустом множестве ее планов.

Теорема: Для того, что бы задача I обладала планами, а задача II планов не имела, необходимо и достаточно, чтобы целевая функция задачи I была не ограничена сверху на множестве ее планов. Для того, чтобы задача II обладала планами, а задача I планов не имела, необходимо и достаточно, чтобы целевая функция задачи II была не ограничена снизу на множестве ее планов.

Например:

 

Задача I Задача II
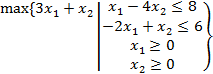
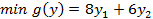при условиях:

 

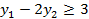
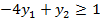
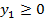
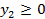
В задаче I 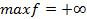; сложив неравенства задачи II получим: 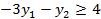. Оно не выполняется ни при каких значениях .

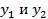И, наконец, случай когда обе задачи I и II не имеют планов.

 

Задача I Задача II
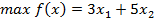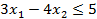
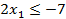
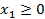
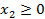
при условиях: 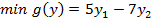при условиях:

 

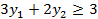
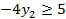
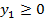
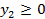
Каждая из I и II задачи не имеет ни одного плана; из 2-го неравенства I задачи вытекает 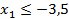; из 2-го неравенства II задачи 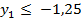(в то время, как они должны быть 0).

Итак, при рассмотрении пары симметричных двойственных задач могут возникнуть 3 случая:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)