Задачи нелинейного программирования с нелинейной системой ограничений и нелинейной целевой функцией

Задача. На множестве решений системы ограничений

+ ≤ 36;

найти глобальные экстремумы функции z = (х - 3)² + (y - 2)².

Решение. Линиями уровня функции z = (х - 3)² + (y - 2)² являются окружности с центром в точке А (3; 2) (рис. 3). Из рисунка видно, что глобальный минимум функция z достигает в точке А (3; 2), а глобальный максимум - в точке В (0; 6). Следовательно

z _min = 0: z _{max = 25.}

Рис. 3.

Задача. Найти глобальные экстремумы функции z = х² + у² на множестве системы ограничений

y ≥ 0.

Решение. На рис. 4 множество допустимых решений заштриховано. Как видно из рисунка, оно не является выпук­лым. Очевидно, что наименьшее значение функция z

достигает в точке В, а наибольшее - в точке К (точка касания окружно­сти

(х - 5)² + (у - 3)² = 36 и линии уровня). Найдем координаты точек В и К. Точка Впринадлежит прямой х + 8 = у и окружности (х - 5)² + (y - 3)² = 9. Поэтому ее координаты находим из системы:

Или

Или

Откуда

или

Получим B (

Точка К принадлежит линии центров 00₁ с уравнением и

окружности 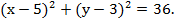Приходим к системе:

т.е. .

В результате получим

.

Таким образом, получим K

Рис. 4.

Следовательно, 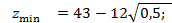. За­метим, что точка F является точкой локального максимума, так как значение функции Zв ней больше, чем значения в сосед­них вершинах В и С. Аналогично, точка С является точкой локального минимума.

Разобранные задачи позволяют нам увидеть ряд особенностей нелинейных задач, которые делают их более трудными для ре­шения, чем линейные задачи. Если система ограничений задачи линейная, а целевая функция нелинейная, то целевая функция может достигать оптиму­ма не обязательно в граничной точке множества допустимых планов, а если она достигает экстремума в граничной точке, то эта точка не обязательно является край­ней. Следовательно, не существует вычислитель­ного метода для задач такого типа, который ограничивался бы только перебором вершин множества допустимых решений. За­метим также, что в некоторых задачах этого типа локальный оптимум не совпадает с глобальным.

В случае нелинейной системы ограничений утверждение о выпуклости области допустимых решений не сохраняется. Если множество допустимых решений не выпукло, то может сущест­вовать отличный от глобального локальный оптимум даже при линейной целевой функци. Следует отметить, что в случае существования локальных оптимумов, отличных от глобальных, нет возможности исполь­зовать вычислительный метод симплексного типа, основанный на переходе от одной вершины к соседней, который оканчивал­ся бы при достижении вершины, доставляющий локальный экстремум целевой функции по сравнению со всеми соседними вершинами.

Для задач нелинейного программирования, имеющих отлич­ные от глобального локальные оптимумы, большинство вычис­лительных методов позволяет найти точку именно локального оптимума. В общем случае они не позволяют установить, сов­падает ли она с точкой глобального оптимума. Тем не менее эти методы отыскания локального оптимума часто оказываются очень полезными на практике. В теории нелинейного программирования особый интерес представляют выпуклые и вогнутые функции. Оказываются справедливыми следующие утверждения:

Пусть F(x) - выпуклая функция, заданная на замкнутом вы­пуклом множестве X. Тогда любой локальный минимум F(x) на Xявляется глобальным минимумом F(x) на X.

Если F(x) - вогнутая функция на замкнутом выпуклом мно­жестве X, то любой локальный максимум F(x) на Xявляется глобальным максимумом.

Поиск по сайту: