Пример. Найти минимум и максимум функции

при условиях:

Решение. Приведём уравнение квадратичной функции к каноническому

виду Целевая функция представляет семейство концентрических окружностей с центром в точке

Построим область допустимых решений. Минимальное значение соответствует наименьшему радиусу окружности и достигается в точке, в которой окружность касается многоугольника О AB. Это точка А (0,1). Максимальное значение соответствует наибольшему радиусу и достигается в наиболее удаленной от точки вершине многоугольника O AB. Это точка B(1,0). Следовательно,

2 .

В этом случае линии уровня являются эллипсами с центрами в точке и канонический вид квадратичной функции будет

При этом полуоси эллипса соотносятся как

Пример. Ре шить задачу методом наискорейшего спуска.

Решение. В качестве исходного приближения берем точку . Вычисляем уклонения точки .

Для нахождения направления спуска ищем частные производные функции в точке :

При этом

Решая задачу линейного программирования

получим

Новое приближение:

Величина шага

Здесь и

- наименьшее положительное число среди отношений

Следовательно

.

Отсюда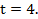

Вычисляем координаты точки

Определяем уклонения точки .

Для нахождения направления спуска решаем задачу линейного программирования:

Решением будут значения При этом

Новое приближение: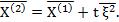

Определим величину шага

Значит, и координаты точки равны:

Определяем уклонение точки

Для нахождения направления спуска решаем задачу линейного программирования

Решением будут значения Следовательно, является оптимальным решением.

Ответ: