Схема решения задачи (1.1) - (1.3) графическим методом

1. Записывают уравнения граничных прямых.

2. Строят графики граничных прямых на плоскости.

3. Выделяют область решения неравенств системы (1.2).

4. Строят многоугольник решений.

5. Строят график линейно формы (1.1).

6. Определяют экстремальную точку многоугольника.

7. Вычисляют значение линейной формы в полученной точке.

Пример. Используя графический метод, найти максимум линейной формы

при условиях:

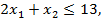
Решение. Записывают уравнения граничных прямых и их графики строят на плоскости в выбранной системе координат:

Выделяют область решения каждого неравенства с помощью вспомогательной точки, в качестве которой удобнее всего взять 0(0,0), и как пересечение построенных полуплоскостей строят многоугольник решений Ω. Выражение линейной формы приравнивают любому произвольному числу и строят график, соответствующий полученному уравнению прямой:

Прямая проходит через начало координат и еще через одну точку, координаты которой легко определить (; (7,5)

Рис. 1.1. Решение задачи линейного программирования графическим методом.

Параллельно перемещая прямую Z в направлении вектора , видим, что экстремальной точкой является точка С (5, 3) – точка пересечения прямых .

Известно, что, система двух линейных уравнений с двумя неизвестными записывается в следующем виде:

где - заданные числа из К.

Матрицы

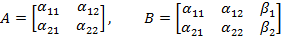
называется соответственной основной и расширенной матрицами системы (1). Чтобы исключить неизвестное 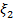, умножим первое из уравнений на 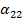, второе на 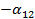и сложим их. В результате получим уравнение

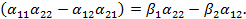
Если 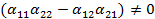, то из этого уравнения и аналогичного уравнения, получающегося путем исключения 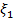, получим

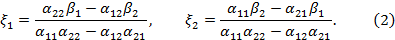
Знаменатели выражений для неизвестных здесь одинаковы и представляют собой многочлен от элементов основной матрицы А. Значение этого многочлена называют определителем или детерминантом матрицы А и обозначают или .

В нашем случае получим

Ответ: max Z = 50, x₁ = 5, x₂ = 3.

При решении задачи линейного программирования графическим методом могут встретиться следующие случаи.

Рис 1). Задача имеет единственное решение

Рис..2). Задача имеет бесконечное множество решений

Рис.3). Линейная форма не ограничена Рис.4). Система ограничений несовместна

Дана общая задача ЛП:

(1)

при условиях:

;

;

;

;

Вводя 4 добавочных неизвестных 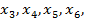получим каноническую систему уравнений ( базис):

Базис ; свободные переменные положим их равными 0.

Пусть тогда 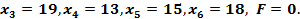В выражении для F можно увеличивать при этом F будет уменьшаться. Примем будет увеличивать до 5, т.к. при этом Поскольку «ненадежнее» всех в базисе, выведем его из базиса, а в базис введем Выразим F и новые базисные переменные через найдём и подставим его в выражения (1), (2), (3).

В итоге получим:

min (*)

при условиях:

.

Допустимое базисное решение следующее: Свободные переменные . Положим их равными 0. Решая пример далее, видим, что увеличивать нельзя, так как будет возрастатать (а нам нужно минимизировать). Значит . Свободную переменную можно увеличивать, но до иначе будет отрицательна .)

Итак, самая «ненадёжная» переменная Выводим из базиса, а вместо её в базис вводим «провокатора» переменную 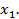Свободные переменные .

Из «ненадёжного» уравнения для

находим

и подставляем *).

Получим:

min

при условиях:

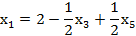
Допустимое базисное решение:

Здесь можно увеличивать до 6, так как

При этом

Достигнуто оптимальное решение: В процессе перехода от одного базисного решения к другому значение F постоянно уменьшалось.