АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задача. Решите ЗЛП методом искусственного базиса: найти максимальное значение при условиях

Читайте также:
  1. В) Задача.
  2. В) Задача.
  3. Задача.
  4. Задача.
  5. Задача.
  6. Задача.
  7. Задача.
  8. Задача.
  9. Задача.
  10. Задача.
  11. Задача.

Решите ЗЛП методом искусственного базиса: найти максимальное значение при условиях

 

Составим матрицу коэффициентов системы уравнений:

 

 

В матрице нет единичных векторов, из которых можно образовать единичную матрицу, т.е. возникает проблема выбора базисных переменных в каждом из уравнений.

Введем искусственные переменные .

 

 

Введем их в целевую функцию с коэффициентами (-М), т.к. решается задача нахождения zmax:

Единичную матрицу образуют коэффициенты при неизвестных х5 и х6, значит эти переменные являются базисными. А так как они являются искусственными переменными, то исходный базис называют искусственным. Переменные х1, х2, х3 и х4 являются свободными.

Таким образом, мы получили расширенную ЗЛП, и будем решать ее симплекс-методом.

Полагая , находим первоначальный опорный план: При этом плане:

1. Заполним первую симплекс-таблицу.

  хБазис     В       -1 -М -М
х3 х4 х5 Х6
х5 -М              
х6 -М              
Δj   -7М -3М-2 -6М-3 -3М-1 -3М+1    

 

min (Δj < 0) = Δ2 = - 6М – 3, значит в базис введем переменную х2.

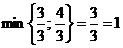, значит, из базиса выводим искусственную переменную х5, поэтому столбец х5 в следующей таблице можно не заполнять.

  1. Производим заполнение второй таблицы по правилам симплекс-метода.

 

 

  хБазис     В       -1 -М
х1 х2 х3 х4 х6
х2     1/3   2/3 2/3  
х6 -М       -1 -1  
Δj   -М+3 -М-1   М+1 М+3  

 

min (Δj < 0) = Δ1 = - М - 1, значит в базис введем переменную х1.

, значит, из базиса выводим искусственную переменную х6, поэтому столбец х6 в следующей таблице можно не заполнять.

2. Заполняем третью таблицу.

хБазис     В       -1
х1 х2 х3 х4
х2   2/3        
х1         -1 -1
Δj            

В третьей таблице обе искусственные переменные оказались равными нулю и все , следовательно, получено оптимальное решение исходной задачи.

Ответ: ,


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)