Модифицированные Жордановы преобразования

Или метод последовательного улучшения плана. Метод предназначен для решения общей задачи линейного программирования.

Пусть имеем следующую задачу:

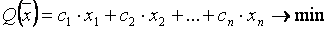, (1)

с системой ограничений следующего вида:

. (2)

Разрешим эту систему относительно переменных :

. (3)

Векторы условий, соответствующие , образуют базис. Перемен­ные назовем базисными переменными. Остальные переменные задачи – небазисные.

Целевую функцию можно выразить через небазисные переменные: .

Если приравнять небазисные переменные нулю ,

то соответствующие базисные переменные примут значения .

Вектор с такими компонентами представляет собой угловую точку многогранника решений (допустимую) при условии, что (опорный план).

Теперь необходимо перейти к другой угловой точке с меньшим значением целевой функции. Для этого следует выбрать некоторую небазисную переменную и некоторую базисную так, чтобы после того, как мы “поменяем их местами”, значение целевой функции уменьшилось. Такой направленный перебор в конце концов приведет нас к решению задачи.

Построение опорного плана. Пусть необходимо решить задачу: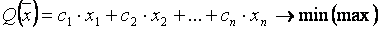

.

Введем дополнительные переменные, чтобы преобразовать ограничения-неравенства к равенствам. В ограничениях-равенствах дополнительные переменные должны быть нулевыми. Тогда система ограничений принимает вид:

,

где .

В качестве базисных переменных будем брать систему дополнительно введенных переменных. Тогда симплексная таблица для преобразованной задачи будет иметь следующий вид:

			….		.…
			….		….
….	….	.…	….	.…	.…	.…	.…
			….		….
			….		….
….	….	….	….	….	….	….	…
			….		….
			….		….

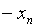
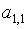
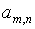
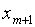
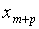
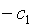
Правила выбора разрешающего элемента при поиске опорного плана.

1. При условии отсутствия “0-строк” (ограничений-равенств) и “сво­бодных” перемен­ных (т.е. переменных, на которые не наложено требованиенеотри­цатель­ности).

· Если в столбце свободных членов симплексной таблицы нет отрицательных элементов, то опорный план найден.

· Есть отрицательные элементы в столбце свободных членов, например . В такой строке ищем отрицательный коэф­фициент , и этим самым определяем разрешающий столбец . Если не найдем отри­цательный , то система ограничений несовместна (противо­речива).

· В качестве разрешающей выбираем строку, которой соответствует минимальное отношение: , где - номер разрешающей строки. Таким образом, - разрешающий элемент.

· После того, как разрешающий элемент найден, делаем шаг модифицированного жорданова исключения с направляющим элементом и переходим к следующей симплексной таблице.

2. В случае присутствия ограничений-равенств и “свободных” переменных поступают следующим образом.

· Выбирают разрешающий элемент в “0-строке” и делают шаг модифицированного жорданова исключения, после чего вычеркивают этот разрешающий столбец. Данную последовательность действий продолжают до тех пор, пока в симплексной таблице остается хотя бы одна “0-строка” (при этом таблица сокращается).

Если же присутствуют и свободные переменные, то необходимо данные переменные сделать базисными. И после того, как свободная переменная станет базисной, в процессе определения разрешающего элемента при поиске опорного и оптимального планов данная строка не учитывается (но преобразуется).

Построение оптимального плана. Для того чтобы опорный план был оптимален, при минимизации целевой функции необходимо, чтобы коэффициенты в строке целевой функции были неположительными (в случае максимизации – неотрицательными). Т.е. при поиске минимума мы должны освободиться от положительных коэффициентов в строке .

Выбор разрешающего элемента. Если при поиске минимума в строке целевой функции есть коэффициенты больше нуля, то выбираем столбец с положительным коэффициентом в строке целевой функции в качестве разрешающего. Пусть это столбец с номером .

Для выбора разрешающей строки (разрешающего элемента) среди положительных коэффициентов разрешающего столбца выбираем тот (строку), для которого отношение коэффициента в столбце свободных членов к коэффициенту в разрешающем столбце минимально: .

– разрешающий (направляющий) элемент, строка – разрешающая.

Для перехода к следующей симплексной таблице (следующему опорному плану с меньшим значением целевой функции) делается шаг модифици­ро­ван­ного жорданова исключения с разрешающим элементом .

Если в разрешающем столбце нет положительных коэффициентов, то целевая функция неограничена снизу (при максимизации – неограниченасверху).

Поиск по сайту: