Симплекс-метод. Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве

Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.

Заметим, что каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый такжеполиэдральным комплексом. Уравнение W (x) = c, где W (x) — максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку — требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Заметим, что пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину, причём, их будет более одной, если пересечение содержит ребро или k -мерную грань. Поэтому максимум функционала можно искать в вершинах многогранника. Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.

Последовательность вычислений симплекс-методом можно разделить на две основные фазы:

1. нахождение исходной вершины множества допустимых решений,

2. последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.

При этом в некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно является допустимым решением, хотя и, скорее всего, далеко не самым оптимальным). В таких задачах первую фазу симплекс-метода можно вообще не проводить. Симплекс-метод, соответственно, делится на однофазный и двухфазный.

Рассмотрим следующую задачу линейного программирования:

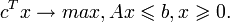
Теперь поставим эту задачу в эквивалентной усиленной форме. Необходимо максимизировать Z, где:

Здесь x — переменные из исходного линейного функционала, x _s — новые переменные, дополняющие старые таким образом, что неравенство переходит в равенство, c — коэффициенты исходного линейного функционала, Z — переменная, которую необходимо максимизировать. Полупространства и в пересечении образуют многогранник, представляющий множество допустимых решений. Разница между числом переменных и уравнений даёт нам число степеней свободы. Проще говоря, если мы рассматриваем вершину многогранника, то это число рёбер, по которым мы можем продолжать движение. Тогда мы можем присвоить этому числу переменных значение 0 и назвать их «непростыми». Остальные переменные при этом будут вычисляться однозначно и называться «простыми». Полученная точка будет вершиной в пересечении соответствующих непростым переменным гиперплоскостей. Для того, чтобы найти т. н. начальное допустимое решение (вершину, из которой мы начнём движение), присвоим всем изначальным переменным x значение 0 и будем их считать непростыми, а все новые будем считать простыми. При этом начальное допустимое решение вычисляется однозначно: .

[править] Алгоритм

Теперь приведём шаги алгоритма. На каждом шаге мы будем менять множества простых и непростых векторов (двигаться по рёбрам), и матрица будет иметь следующий вид:

где c _B — коэффициенты вектора c соответствующие простым переменным (переменным x _s соответствуют 0), B — столбцы , соответствующие простым переменным. Матрицу, образованную оставшимися столбцами обозначим D. Почему матрица будет иметь такой вид поясним в описании шагов алгоритма.

Первый шаг.

Выбираем начальное допустимое значение, как указано выше. На первом шаге B — единичная матрица, так как простыми переменными являются x _s. c _B — нулевой вектор по тем же причинам.

Поиск по сайту: