Аналитический метод решения задачи. Условия максимума функции одной переменной

Пусть 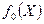- непрерывная и дважды дифференцируемая функция при 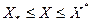и X⁰ - точка предполагаемого маусимума функции. Для того, чтобы при X⁰ функция достигала max необходимо, чтобы при любом другом Х, сколь угодно близком к X⁰, т.е. , выполнялось соотношение (2.3)

Разложим 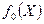в ряд Тейлора в окрестности точки X⁰

(2.4)

При небольших DХ, членами, содержащими приращения в степени больше единицы можно пренебречь и тогда из (2.4) следует:

. (2.5)

Подставляя (2.5) в (2.3) окончательно получаем необходимое условие максимума функции одной переменной:

(2.6)

При использовании этого условия могут возникнуть два варианта:

1. - внутренняя точка интервала допустимых значений (рис. 2.3). В этом случае знак DХ не определен и для выполнения условия (2.6) необходимо

(2.7)

При этом знак разности (2.3) определяется знаком первого отброшенного члена ряда Тейлора, т.е. знаком 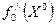. Поэтому необходимое условие max (2.7) дополняется условием

(2.8)

2. - граничная точка интервала 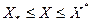. В этом случае знак DХ определен (рис. 2.4) и для расчетов будем использовать выражение (2.6).

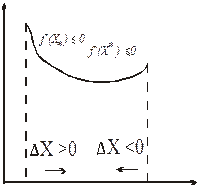
Рис.2.3. Х_* Х^* Х

Рис. 2.4.

Сформулируем правила применения необходимых условий максимума функции одной переменной.

1. Определяют все корни уравнения (2.7), являющиеся внутренними точками отрезка 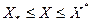и для каждого из них проверяют условие (2.8). Удовлетворяющие ему корни являются точками локальных максимумов целевой функции.

2. Рассчитывают значение функции 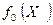в этих точках и сравнив их между собой определяют глобальный максимум.

3. Если среди корней уравнения (2.7), нет значений, принадлежащих множеству допустимых решений, необходимо проверить граничные точки и с использованием условия (2.6).

Пример. Определить максимум функции при

а) , б) , в) ;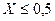

а) X⁰ = 0.6, внутренняя точка отрезка , следовательно, знак ΔX не определен и необходимо проверить выполнение условия (2.8).

< 0

Условие (2.8) выполняется.

Ответ:

б) 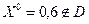, проверим 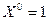- нижняя граница отрезка , следовательно, DХ > 0.

Проверяем выполнение условия (2.6).

< 0.

Условие (2.6) выполняется, т.е. .

в) 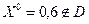. Проверим Х = 0.5 – верхняя граница отрезка 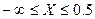, следовательно, DХ < 0.

Проверяем выполнение условия (2.6): > 0

Условие (2.6) выполняется, т.е.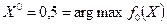

Поиск по сайту: