Оптимизация циклического установившегося режима

Для циклических режимов критерием оптимальности является среднее значение целевой функции ¦₀ за период цикла T:

I = dt ® max (9.9)

Связи между переменными состояния 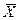и управляющими воздействиями 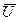характеризуют динамику процесса и имеют форму дифференциальных уравнений (9.4), автономные ограничения (9.2) остаются в силе, а ограничения на ресурс управляющих воздействий задаются в среднем за цикл, т.е.

dt - b_m = 0 m = 1, …, r (9.10)

Они могут соответствовать ограничениям на средний расход сырья, электрической энергии и т.п.

Краевые условия типа (9.3) для дифференциальных уравнений (9.4) в циклическом режиме, как правило, не фиксированы, однако ввиду непрерывности переменных и их периодичности справедливы равенства:

Xn(T) = Xn(0) n = 1,…m (9.11)

что эквивалентно требованиям

dt = 0 n = 1,…, m (9.12)

В этой задаче кроме законов изменения управляющих переменных и связанных с ними переменных состояния, нужно ещё оптимально выбрать длительность цикла T.

Часто форму изменения управляющих воздействий задают с точностью до нескольких параметров. Например, считают их синусоидальными. Тогда нужно найти амплитуды и средние значения управляющих переменных, а также фазовые сдвиги между ними.

Поиск по сайту: