АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример постановки вариационной задачи

Читайте также:
  1. I. 1.1. Пример разработки модели задачи технического контроля
  2. II. Подкожная инъекция. Область постановки, техника выполнения процедуры. Осложнения.
  3. IV. ТИПОВОЙ ПРИМЕР РАСЧЕТОВ.
  4. X. примерный перечень вопросов к итоговой аттестации
  5. А. Постановка транспортной задачи.
  6. Алгоритм постановки газоотводной трубки.
  7. Алгоритм постановки диагноза ХСН
  8. Алгоритм постановки лекарственной клизмы
  9. Аналитический метод решения задачи.
  10. Аналитический метод решения задачи. Условия максимума функции одной переменной.
  11. Б. Математическая модель транспортной задачи.
  12. Б2. Пример №2

Как указывалось выше (см. раздел 1.3), функционалом называется функция, аргументом которой является другая функция. Функционал обычно формируется в виде интеграла, определенного в некоторых пределах, и решить вариационную задачу, значит найти выражение функции, которая обеспечит максимум этого интеграла.

Рассмотрим постановку и решение оптимизационной задачи на простейшем примере.

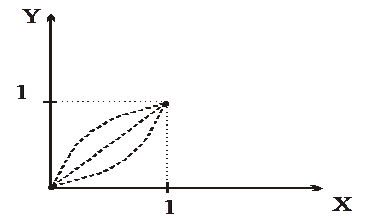
Пример. Определить уравнение, описывающее функцию, график которой проходит через две заданных точки и имеют между ними наименьшую длину.

 

 

.

 

Рис. 7.1

Пусть одна из точек находится в начале координат , а другая в точке с координатами . - функция, проходящая через две точки (рис. 7.1), - элементарный участок функции

Рис.7.1.

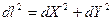
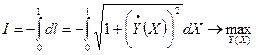
Знак «минус» появился перед интегралом при переформулировании задачи нахождения минимума на задачу нахождения максимума.

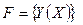- функционал, - экстремаль (максималь или минималь) - искомое уравнение функции, обеспечивающее экстремум функционала.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)