Оптимизация режима в аппарате периодического действия

Здесь сырьё периодически загружают в аппарат, а готовый продукт периодически выгружают из него. Продолжительность цикла, а также закон изменения управляющих воздействий за время цикла подлежат оптимальному выбору.

Пусть целевая функция ¦₀(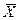, 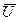) определяет мгновенную продуктивность процесса.

Обозначим через q - продолжительность загрузки и выгрузки, а T – продолжительность работы аппарата в каждом цикле. Учтём также, что загрузка и выгрузка связаны не только с затратами времени, но и с затратами трудовых и материальных ресурсов на сырьё, очистку аппарата и т.д. Величину этих затрат, которые обычно не зависят от длительности цикла, обозначим через А.

Тогда критерий оптимальности задачи запишется в виде:

I = dt – А) ® max (9.13)

Максимум этого выражения нужно найти при условиях (9.4), записанных в форме дифференциальных уравнений и при фиксированных начальных значениях переменных состояния.

X _n(0) = X _n0 n = 1,…, m (9.14)

Что касается конечных значений этих переменных X n(T), то, как правило, некоторые из них фиксированы, а остальные свободны.

X _n(T) = X _nT n = 1,…, k; k < m (9.15)

Условия типа автономных ограничений (9.2) и функциональных ограничений (9.5) также могут иметь место. Выбору подлежат управляющие воздействия 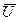(t) и рабочее время цикла T.

9.6. Календарное планирование работы аппарата

В предыдущих задачах предполагалось, что собственные характеристики аппарата и условия, в которых он работает, неизменны. В действительности же и те и другие могут изменяться во времени. Например, по некоторому закону могут изменяться заданная производительность и поставки сырья. Как правило, эти изменения происходят значительно медленнее, чем переходные процессы в аппарате, поэтому связи между состояниями X и управлениями U задают в квазистатической форме.

¦n(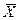, , 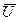t) = 0 n = 1,…, m (9.16)

Производительность аппарата для каждого момента времени t должна лежать в заданном интервале

P_*(t) £ P (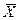, 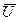) £ P^*(t) (9.17)

Если в аппарате имеются ёмкости, то на уровень в них наложены ограничения H_{i *} £ H_i (t) £ H_i ^* " t

_·

H_i = h_i (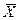, , 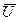t) i = 1 ,…, l, (9.18)

где h_i (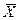, , 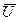t) – разность потоков, втекающих в i -ю ёмкость и вытекающих из неё в момент t.

Если через T_n обозначить интервал планирования, то критерием оптимальности может служить интегральная эффективность аппарата за этот интервал.

I = dt ® max (9.19)

Поиск по сайту: