Определение безусловного максимума функционала

(Классическая вариационная задача), (задача Эйлера).

Постановка задачи:

(7.1)

Необходимое условие оптимальности определяется уравнением Эйлера.

(7.2)

Из выражения (7.2.) вытекают два частных случая:

Если явно не зависит от , то (7.3)

Если явно не зависит от , то , (7.4)

откуда следует (7.5)

Условие (7.2) дополняется следующим условием Лежандра

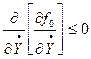(7.6)

Если выполняются условия (7.2) и (7.6), то - максималь.

Рассмотрим решение примера, условия которого сформулированы в разделе 7.1.

Так как подынтегральная функция 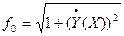не зависит явно от Y, то используем условие оптимальности Эйлера (7.5). Внеся минус под знак интеграла, получим.

, откуда получаем

,

, следовательно, ;

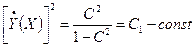Отсюда следует, что .

Интегрируя, находим , где С ₃ – постоянная интегрирования.

Для нахождения значений С ₂ и С ₃ используем начальные условия задачи, т.е. координаты заданных точек: Y = 0 при X = 0, следовательно С ₃ = 0; Y = 1 при X = 1, следовательно С ₂ = 1.

Окончательно получаем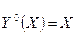

Проверка условия Лежандра. Учитывая, что (X)=1, имеем:

т.е. - максималь, что и требовалось доказать.

Поиск по сайту: