 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод крутого восхождения
Метод крутого восхождения отличается от метода градиента правилом определения коэффициента шага γ.
Он должен быть таким, чтобы f0 достигала max по направлению градиента при данном значении γ, т.е.
=arg max 
(3.12).
где k = 1,2,3…- номер шага поиска
Поясним это требование на примере рис.3.8. Помня о том, что чем ближе сомкнуты линии равного уровня к максимуму тем большему значению целевой функции они соответствуют, можно сделать вывод, что целевая функция при движению по градиенту из точки A, будет возрастать примерно до точки С, а при дальнейшем движении начнет уменьшаться.
Таким образом в методе крутого восхождения ставится задача расчета такой величины коэффициента шага 
, чтобы за один шаг попасть из точки А в точку С.
Пример:
Для f0(
) = -X12 + X1 X2 - X22 + X1 выполнить один шаг поиска максимума из начальной точки (0) с координатами X1 (0)=5, X2 (0)=2, методом градиента и методом крутого восхождения
I. Метод градиента:
1. Рассчитываем проекции вектора градиента в начальной точке
а 1(0) = 
= (-2 X1 + X2 +1) 
= -2 • 5 + 2 + 1 = -7
а 2(0) = 
= (X1- 2 X2) = 5 – 2 • 2 = 1
2. Выбираем для первого шага γ1=0,3
3. Рассчитываем координаты точки (1) после первого шага по выражению (3.8)
X 1(1) = X 1(0) + γ1 a 1(0) = 5 + 0,3 • (-7) = 2,9
X 2(1) = X 2(0) + γ1 a 2 (0) = 2 + 0,3 • 1 = 2,3.
4. Определяем проекции вектора градиента в точке (1)
а 1(1) =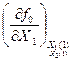 
= -2 • 2,9 + 2,3 + 1 = -2,5
а 2(1) = 
= 2,9 – 2 • 2,3 = -1,7
5. Вычисляем модули градиента в точках (1) и (0)
6. Определяем cos α
сos α= 
= 
Условие (3.10) не выполняется, необходимо уменьшить шаг. Выбираем γ1=0,2 и пересчитываем.
Поскольку проекции вектора градиента а 1(0)=-7 и а 2(0)=1 в исходной точке остались теми же самыми, сразу определяем координаты первой точки, т. е. повторяем пункт 3 расчета при значении γ1=0,2.
(1)=5+0,2*(-7)=3,6
(1)=2+0,2*1=2,2
Определяем проекции вектора градиента в точке (1), аналогично пункту 4
а 1(1)=-2*3,6+2,2+2=-4
а 2(1)=3,6-2*2,2=-0,8
Вычисляем модуль градиента в точке (1) и пересчитываем значение cos α, аналогично пунктам 5 и 6.
сos α= 
Условие (3.10) выполнено, следовательно, для первого шага выбираем коэффициент γ1=0,2.
Рассчитываем значения целевой функции в нулевой и первой точках.
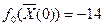
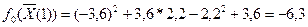
Значение целевой функции после первого шага возросло, следовательно, расчет сделан правильно.
II. Метод крутого восхождения.
По выражению (3.8) определяем координаты первой точки (1) как функции от коэффициента шага γ1, используя значения проекций вектора градиента, рассчитанных выше.
(1)= (0)+γ1 a 1(0)=5+ γ1*(-7)=5-7 γ1
(1)= (0)+γ1 a 2(0)=2+ γ1*1=2+ γ1
Подставляем полученные выражения (1), (1) в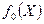 
. Необходимо, чтобы полученное выражение достигало max по γ1.
(γ1)=-(5-7γ1)2+(5-7γ1)(2+γ1)-(2+γ1)2+(5-7γ1)→max
Для этого производная 
должна быть равна нулю.
=-2(5-7 γ1)*(-7)+(-7)(2+ γ1)+(5-7 γ1)-2(2+ γ1)+(-7)=0
Отсюда γ1=0,44.
По выражению (3.8) определяем координаты первой точки (1)
(1)=5-0,44*7=1,93
(1)=2+0,44*1=2,44
Вычисляем значение целевой функции в точке (1) и сравниваем его со значением в точке (0), вычисленным ранее.
> 
Сравнивая значения целевой функции после первого шага вычислений двумя рассмотренными методами
а также объем вычислений на этом шаге, приходим к выводу о большей эффективности метода крутого восхождения.
4. Определение условного максимума функции нескольких переменных.
Методы нелинейного программирования
Поиск по сайту: