Принцип оптимальности Беллмана

Предназначен для решения задачи (5.1) – (5.4) оптимизации многостадийных процессов.

При заданном начальном состоянии процесса стратегия управления однозначно определяет состояние многостадийного процесса на всех стадиях, т.к. любое можно последовательно рассчитать по уравнению связи (5.11)

Беллман сформулировал следующий принцип оптимальности, который позволяет определить оптимальную стратегию управления без использования метода неопределенных множителей Лагранжа:

Оптимальная стратегия обладает тем свойством, что какова бы не была последовательность , приводящая к состоянию , управление должно быть оптимальным по отношению к этому состоянию как исходному. Поясним принцип оптимальности Беллмана на примере похода в лес за грибами.

В процессе поиска грибов человек перемещается по лесу достаточно хаотично, руководствуясь соображениями типа: туда пойду – там березки, туда не пойду – там овраг. Однако, приняв решение возвращаться домой, грибник старается с этого момента, т.е. из промежуточного состояния X_i-1, двигаться оптимально, чтобы добраться домой за наименьшее время, в какую бы точку леса его ни привело управление своим движением на предыдущих этапах.

Функцией Беллмана называется оптимальное значение целевой функции для стадий процесса с i -й до n -ой включительно. Оно, очевидно, должно зависеть от состояния объекта .

(5.12)

Выделим в правой части выражения (5.12) первое слагаемое под знаком max

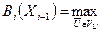
, (5.13)

где (5.14)

Подставляя вместо 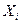в соответствии с уравнением связи (5.11), с учетом того, что 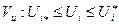получаем уравнение Беллмана.

(5.15)

Очевидно, что после окончания процесса, управление отсутствует, т.е.

(5.16)

Уравнение (5.15) совместно с граничным условием (5.16) позволяет решать задачи оптимизации многостадийных процессов от конца к началу.

Поиск по сайту: