Задача определения оптимального пути на сетевом графике (графе)

Сетевые графики используются для решения дискретных задач оптимизации многостадийных процессов, в которых переменные управления могут принимать только несколько определенных значений. Пример сетевого графика представлен на рис. 5.3.

Рис. 5.3.

Задача заключается в том, чтобы из заданного начального состояния попасть в заданное конечное состояние , следуя тем путем для которого суммарное управление, т. е. сумма цифр, поставленных над дугами графа (значений ) была максимальна. Таким образом, структурная схема данной задачи, представленная на рис. 5.4, аналогична структурной схеме задачи оптимизации многостадийных процессов (см. раздел 5.1).

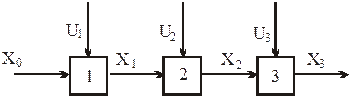
Рис. 5.4.

Рассмотрим решение поставленной задачи на примере сетевого графика (графа), представленного на рис 5.5.

Рис. 5.5.

Найти при котором 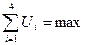. Задача решается от конца сетевого графика к началу, т. е. справа налево.

1) Рассмотрим все состояния четвертой стадии. Согласно принципу оптимальности Беллмана, в каком бы из них процесс не оказался, далее следует действовать оптимально. В данном случае управление единственно для каждого , К=1,2,3,4, а значит оно и оптимально. Ему соответствует единственное, а значит и максимальное значение управления. Это значение мы впишем внутрь кружка соответствующего каждому из состояний и обозначим: , , , , 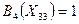а дугу, соответствующую оптимальному движению в , подчеркнем штриховой линией и будем называть ее условно оптимальным управлением (оптимальным при условии, что мы оказались в данном состоянии).

2) Переходим к следующей, т.е. третьей стадии. Для каждого из возможных состояний , К =1,2,3,4, ищем оптимальное решение, приводящее к c максимальным значением U на двух последних стадиях. Для каждого из этих состояний возможны три управления. Так для первого управления из состояния получаем и , пять записано в кружочке, это самое лучшее, что можно получить, если мы окажемся в . Т.о. первое управление даст второе 8 и третье 4. Следовательно, оптимальным по отношению к является первое управление, а максимальное значение . Обозначим его через и занесем 9 внутрь кружка, а условно оптимальное управление подчеркнем штриховой линией. Аналогично найдем условно-оптимальное управление по отношению к состоянию как к начальному и подсчитаем максимальное управление для этого состояния B₃ (X₂₂) = 7. Для остальных состояний третьей стадии получаем 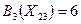, - запишем эти значения в кружочках.

3) Переходим ко второй стадии и для каждого состояния К=1..4 подсчитаем максимальное управление при условии, что это состояние является начальным и определим соответствующее ему условно-оптимальное управление . Отметим, что при этом мы будем пользоваться лишь функцией , значение которой уже рассчитано на предыдущем этапе и записано внутри кружков соответствующих . Получим В₂ (X₁₁)=7+9=16, В₂ (X₁₂)=5+7=12, В₂ (X₁₃)=4+9=13, В₂ (X₁₄)=3+8=11.

4) Для первой стадии, т.е. для начального состояния , выбор оптимального управления производится один раз, т.к. это состояние задано, причем условно-оптимальное решение на этот раз будет искомым оптимальным решением поставленной задачи, а величина представляет собой максимальное суммарное управление. Найденное управление ведет в состояние , для которого управление уже найдено и т.д. Таким образом, задача решена. В результате на сетевом графике получим оптимальную траекторию (подчеркнута сплошной двойной линией), обеспечивающую перевод процесса из заданного начального состояния X₀ в заданное конечное состояние X₄ с max затратами на управление

Очевидно, что такая задача была поставлена только для пояснения принципа расчета сетевых графиков. В реальных задачах требуется обеспечить min расходы на суммарное управление, однако порядок расчета при этом не изменится.

Обобщим процедуру решения примера. Отметим, что величина оптимального суммарного управления подсчитывалась как максимальнаяпо суммы двух слагаемых: управления на i -й стадии и максимумуправления, подсчитанного ранее при условии, что мы попадаем в состояние 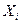. Т.о. имеем уравнение Беллмана:

Для рассмотренного примера имеем:

, , , , .

, , , .

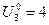Поиск по сайту: