АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Определение условного максимума функционала

Читайте также:
  1. Access. Базы данных. Определение ключей и составление запросов.
  2. I. Дифракция Фраунгофера на одной щели и определение ширины щели.
  3. I. Определение
  4. I. Определение
  5. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  6. I. Определение пероксида водорода (перекиси водорода)
  7. I. Определение проблемы и целей исследования
  8. I. Определение ранга матрицы
  9. I. Пограничное состояние у новорожденных детей. Определение, характеристика, тактика медицинского работника.
  10. I. Сестринский процесс при гипертонической болезни: определение, этиология, клиника. Принципы лечения и уход за пациентами, профилактика.
  11. I. Сестринский процесс при диффузном токсическом зобе: определение, этиология, патогенез, клиника. Принципы лечения и ухода за пациентами
  12. I. Сестринский процесс при остром инфаркте миокарда: определение, клиника, неотложная помощь, транспортировка пациента.

(неклассическое вариационное исчисление)

(7.7)

(7.8)

Для решения задачи (7.7), (7.8) используется метод, аналогичный методу неопределенных множителей Лагранжа. Составляется функционал Лагранжа.

Доказано, что если функция является решением задачи (7.7), (7.8), то найдется такое значение , при котором 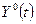обеспечивает безусловный максимум функционала Лагранжа.

Таким образом, необходимым условием оптимальности для задачи (7.7), (7.8) является условие максимума функции L по 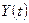,.т.е.

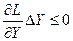(7.9)

В частности, если автономные ограничения отсутствуют, то условие (7.9) сводится к

(7.10)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)