Метод дихотомии. (Метод деления интервала неопределенности пополам)

(Метод деления интервала неопределенности пополам)

Идея метода заключается в том, чтобы делить интервал неопределенности пополам и по результатам каждой итерации отбрасывать ту половину, где максимума быть не может.

Для этого достаточно вычислить значения f₀(x) в точках 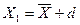и , где , , - допустимая погрешность определения максимума. И сравнить их между собой.

Проиллюстрируем порядок расчета с помощью рис. 2.7

Рис. 2.7

Для функции, показанной на рис. 2.7, на первой итерации расчета

> , поэтому отбрасываем правую часть интервала неопределенности, делаем переприсвоение X^* = ,

Рассчитываем новые значения , , 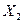затем значения , и сравниваем их между собой. На второй итерации расчета

(рис. 2.7), поэтому отбрасываем левую часть интервала неопределенности и делаем переприсвоение Х _* = и т. д.

Вычисления заканчиваются, когда интервал неопределенности становится меньше допустимой погрешности e, и за решение принимается наибольшее из двух последних вычисленных значений или .

Определим количество вычислений целевой функции, необходимое для нахождения точки максимума методом дихотомии с заданной точностью.

На каждой итерации интервал неопределенности уменьшиться в два раза, т.е.

За n итераций имеем

Для обеспечения требуемой точности расчета должно быть

, откуда .

Логарифмируя, получаем выражение, определяющее число итераций расчета, требуемое для решения задачи с заданной погрешностью .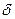

;

Общее количество расчетов целевой функции при этом N_D=2n.

При получаем , откуда n=10 и .

Поиск по сайту: