 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Симплекс-метод. При использовании этого метода направление очередного шага поиска определяется в зависимости от значения целевой функции в вершинах выпуклого многогранника
При использовании этого метода направление очередного шага поиска определяется в зависимости от значения целевой функции в вершинах выпуклого многогранника, называемого симплекс. При n-переменных симплекс имеет (n +1) вершину. В двумерном пространстве (n =2) симплексом является треугольник. Симплекс называется регулярным, если размеры всех его граней одинаковы.
Из любого симплекса, отобразив одну из его вершин симметрично, относительно противоположной грани, можно получить новый симплекс.
Алгоритм поиска максимума состоит в следующем:
1. Строится исходный симплекс S0, который включает в себя в качестве одной из вершин исходную точку 
. По заданной длине грани определяют координаты остальных вершин и значения функции ¦0 во всех вершинах.
2. Следующий симплекс S1 строится зеркальным отображением вершины с минимальным значением целевой функции относительно противоположной грани.
3. Определяют значения ¦0 в вершинах симплекса S1, строят симплекс S2 и т.д.
Доказано, что при этом центр симплекса движется в сторону точки максимума целевой функции, вблизи от которой происходит зацикливание. Наличие зацикливания – признак приближения к максимуму и может быть использовано как условие для завершения вычислительной процедуры. Скорость поиска и точность зависят от размера грани, чем она больше, тем скорость выше, а точность меньше. Поэтому на практике используют модификации симплексного метода, в которых размер грани уменьшается, по мере приближения к точке максимума. Условием окончания поиска может служить уменьшение грани симплекса до заданной величины e.
Вычисление координат отражённой вершины каждого следующего симплекса осуществляется по формуле:
(3.7),
где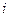 
- i-тая координата 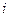=1,2… 
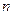, отражённой j-той вершины 
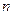= 1, 2, …, ( +1).
Пример:
Определить max функции 
Принять начальную точку с координатами 
= 2, 
= 0 и 
– длина грани. Задача двумерна, следовательно, симплексом является треугольник.
Рис. 3.7
Последовательность решения задачи геометрически представлена на
рис. 3.7. Результаты расчетов сведены в таблицу.
Таблица
| № верш. | X1 | X2 | ¦0 |
| 2.5 | 0.865 | 21.5 | |
| 11 | 3.5 | 0.865 | 25.5 |
| 22 | 1.73 | ||
| 33 | 1.73 | ||
| 14 | 3.5 | 2.6 | 26.4 |
Строим симплекс S0, определяем координаты его вершин 1, 2, 3, рассчитываем значения целевой функции f0 в вершинах и заносим результаты в таблицу. Наименьшее значение f0 =16 получается для вершины 1, поэтому отображаем эту вершину симметрично, относительно противоположной грани, рассчитываем координаты отображенной вершины 11 в соответствии с выражением (3.7) и строим симплекс S1. При расчетах координат отображенных вершин 
будем пользоваться следующими обозначениями:
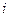- номер координаты;
- номер вершины;
- номер отображения;
то есть 
- это вторая координата первой вершины после первого отображения и т.д., причем отображения нумеруются подряд, независимо от того, какая вершина отображается.
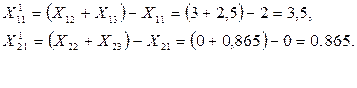
Вершинами S1 являются точки 2, 3,11. Так как значения f 0 в вершинах 2 и 3 уже известны, рассчитываем только значение целевой функции в вершине 11. Результаты расчетов заносим в таблицу. Сравнивая значения f 0 в вершинах симплекса S1, получаем наименьшее значение f 0 = 21 для вершины 2, поэтому отображаем эту вершину, аналогично предыдущей, рассчитываем координаты отображенной вершины 22 и строим симплекс S2, вершинами которого являются точки 3, 11, 22.
 |
Проведя аналогичные операции с симплексом S2, получаем симплекс S3 с вершинами 11, 22, 33, а затем и симплекс S4 с вершинами 22, 33, 14.
Для симплекса S4 минимальным является значение целевой функции в вершине 14 (см. таблицу). Поэтому для построения следующего симплекса S5 необходимо отобразить вершину 14 и таким образом S5 будет совпадать с S3, т.е имеет место зацикливание. Для повышения точности расчёта целесообразно уменьшить грань симплекса, стянув его к вершине с б о льшим значением целевой функции f0 (вершина 33 ), например путем деления первоначальной длины грани пополам (см. рис. 3.7).
После чего процедура поиска продолжается. Расчёт заканчивается, когда зацикливается симплекс с размером грани меньше заданного e, и за решение задачи принимаются координаты вершины последнего симплекса, с максимальным значением целевой функции.
Поиск по сайту: