АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод золотого сечения. Интервал неопределенности делится на три отрезка, причем внутренние точки располагаются симметрично по отношению к крайним (рис

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.2. Двойственный симплекс-метод.
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. Метод рассмотрения остатков от деления.
  8. I. Методические основы
  9. I. Методические основы оценки эффективности инвестиционных проектов
  10. I. Организационно-методический раздел
  11. I. Предмет и метод теоретической экономики
  12. I. Что изучает экономика. Предмет и метод экономики.

Интервал неопределенности делится на три отрезка, причем внутренние точки располагаются симметрично по отношению к крайним (рис. 2.8), таким образом, чтобы выполнялось соотношение 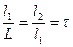(2.10)

 

 

 
Рис. 2.8

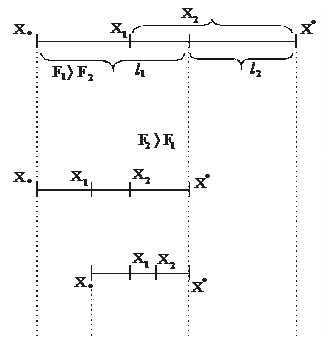
Величина 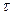определяется следующим образом. Из (2.10), с учетом того, что 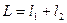, получаем 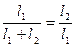, откуда 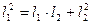(2.11)

Разделив обе части выражения (2.11) на 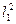, получим

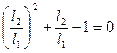(2.12)

С учетом (2.10) из (2.12) имеем 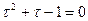, откуда

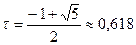- золотое сечение.

Рис. 2.8
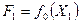Далее вычисляем значения и 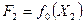. Если 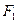> 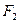, то интервал неопределенности сокращается путем отбрасывания правого отрезка, а если 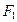< 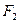, то левого (см. рис. 2.8). Расчет повторяется до тех пор, пока после очередного этапа 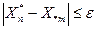, и за решение принимается наибольшее из двух последних вычисленных значений F1 или F2.

Т.к. 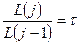, то 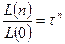, где n - число итераций расчета.

В случае задания допустимой погрешности как 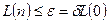, имеем

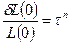(2.13).

После сокращения левой части (2.13) на L(0) и логарифмирования, получаем 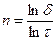, Nзс=n+1 – общее число вычислений целевой функции.

При , , .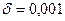

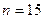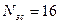Сравнивая требуемое количество расчетов целевой функции для решения задачи одномерной оптимизации разными методами с одной и той же допустимой погрешностью , получаем

.

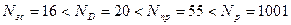Заметим, что метод золотого сечения более эффективен, с точки зрения требуемого объема вычислений, по сравнению с методом дихотомии, в котором на каждой итерации необходимо два раза вычислять целевую функцию, а в методе золотого сечения на всех итерациях кроме первой целевая функция вычисляется только один раз, а второе сравниваемое значение целевой функции берется из предыдущей итерации.

Так, из рис. 2.8. имеем, f0 (X1) на первой итерации равно f0 (X2) на второй итерации равно f0 (X1) на третьей итерации и т.д.

Таким образом, можно сделать вывод, что развитие методов одномерного поиска было направлено исключительно на уменьшениеобъема вычислений, необходимых для решения оптимизационных задач.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)