Приближение к идеалу

Пусть известны решения m задач оптимизации вида

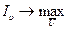; υ=1, …, m (8.4)

В результате найдены предельные значения каждого из частных критериев оптимальности без учета остальных. В пространстве критериев точку 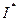с координатами называют идеалом. Когда решения задач (8.1) не одинаковы, идеал не принадлежит множеству допустимых значений критериев (см. рис. 8.1).

Однако можно на втором этапе решения поставить задачу определения такого достижимого критерия и соответствующего ему допустимого решения , для которых расстояние от идеала было бы минимальным, например

(8.5) или

(8.6)

В случае выбора критерия (8.5) минимизируется квадрат расстояния от достижимой оптимальной точки на плоскости критериев до точки идеала I^*, при выборе критерия (8.6) минимизируется максимальное из расстояний от получаемой точки до точек максимума по частным критериям I₁^* или I₂^*.

Поиск по сайту: