Классификация оптимизационных задач

Приведем классификацию оптимизационных задач по характеру искомого решения (рис. 1.4). Это задачи о безусловном максимуме функции одной и нескольких переменных, решением их является вектор 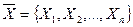, где X₁, X₂, …,Х_n – значения варьируемыхпеременных, причем на эти переменные не наложено никаких ограничений, либо наложены автономные ограничения .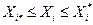

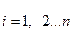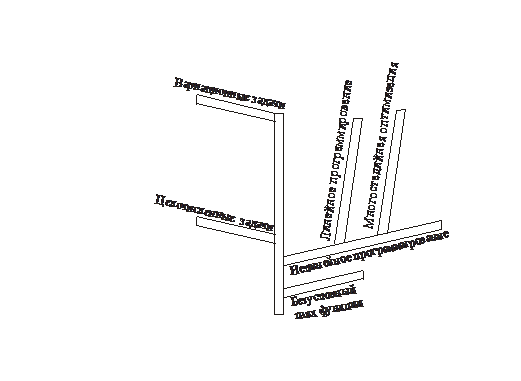
Рис. 1.4

Задачи об условном максимуме функций называют задачами математического программирования, в общем случае нелинейного программирования. Их решением также является вектор 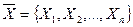, причем в этом случае на варьируемые переменные X₁, X₂, …,X_n накладываются ограничения типа связи в виде равенств j_j ( ) = 0, j = 1,2,...,m и (или) функциональные ограничения в виде неравенств y_к ( ) £ 0, k=1,2,…,r, где j_j ( ) и y_к ( ) – функции, которые определяются из условий решаемой оптимизационной задачи. Автономные же ограничения могут как присутствовать, так и отсутствовать.

Важным частным случаем такой задачи является задача линейного программирования, в которой критерий оптимальности и ограничения линейно зависят от варьируемых переменных. Суть задачи оптимизации многостадийных процессов состоит в определении оптимальной стратегии управления, т.е. оптимальной последовательности управляющих воздействий на каждом этапе (стадии) процесса.

Если значения искомых переменных могут принимать лишь целочисленные значения, то задачу называют целочисленной или комбинаторной. Параметром такой задачи может служить задача оптимального планирования грузоперевозок, в которой нужно распределить имеющиеся количество автотранспорта по различным маршрутам.

Наконец, если решением задачи является функция, то задачу называют вариационной или задачей об оптимуме функционала.

Поиск по сайту: