Оптимальность по Парето

Выбор любого сводного критерия субъективен или основан на некоторых дополнительных предположениях. Однако оптимальное решение в задаче с несколькими критериями можно получить без введения сводного критерия. Такой подход был предложен в 1904 г. итальянским экономистом В. Парето.

Оптимальным по Парето решением Uп является любое решение, если среди допустимых решений не найдётся такого U^О, для которого:

I _υ(U ^O) ³ I _υ(U _п) υ= 1,…,m (8.10)

причём хотя бы для одного значения υ неравенство (8.10) строгое. Иными словами, U_п оптимально, если, изменяя его, нельзя улучшить ни одного из частных показателей, не ухудшая при этом хотя бы одного из остальных.

Оптимальным, по Парето, решениям соответствует на рис. 8.1 та часть границы множества I (выделена жирной линией), для которой любое направление движения, образующее с осью абсцисс угол от 0 до p/2, выходит за пределы множества I, например, точка I_п1.

Можно доказать, что любой из приведённых выше способов образования сводного критерия I приводит к получению одного из решений, оптимальных по Парето. В том случае, когда граница множества I, соответствующая оптимальным по Парето решениям, выпукла, все эти решения можно получить из задачи о максимуме сводного критерия (8.1) при изменении весовых коэффициентов g_υ, т.е. в пределах условий (8.2).

Действительно, для рис. 8.1 в соответствии с выражениями (8.1) и (8.2) имеем:

В случае , , 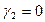получаем , а при , . Очевидно, что при уменьшении от единицы до нуля и соответствующем увеличении от нуля до единицы точка будет перемещаться по границе множества I от точки 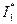до точки .

Поиск по сайту: