АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Свертка частных критериев с весовыми коэффициентами

Читайте также:
  1. Аддитивная свертка критериев
  2. Анализ различных критериев периодизации психического развития. Понятие ведущей деятельности
  3. Анализ частных случаев.
  4. Бюджетный дефицит можно классифицировать по ряду критериев.
  5. В сферу частных и корпоративных (общественных) интересов
  6. Взвешивание критериев
  7. Взносы на обязательное страхование от несчастных случаев на производстве и профессиональных заболеваний
  8. Вопрос. Дискретная свертка
  9. Выбор и разработка экологических критериев продукции
  10. Выполнение «пропускных критериев» участия в «зоне евро» ее
  11. Г.Сумме частных инвестиций и амортизации
  12. Глава 4. ЗАЩИТА ПРАВ ЧАСТНЫХ СУБЪЕКТОВ 1 страница

В этом случае сводный критерий I представляет собой сумму частных критериев , умноженных на соответствующие весовых коэффициенты .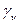

Весовые коэффициенты 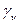учитывают относительную важность того или иного критерия и устанавливаются путем экспертизы для конкретной задачи оптимизации. Причем их значения должны лежать в переделах от нуля до единицы, а их сумма равняться единице.

Математическая постановка задачи:

(8.1)

где ; (8.2)

Значения частных критериев при формировании сводного критерия должны быть либо безразмерными, либо иметь одинаковую размерность, для того, чтобы их суммирование имело смысл.

Геометрически, применение критерия (8.1) приводит к выбору на множестве I такого вектора у которого максимальна проекция на прямую γ, такую, что квадраты ее направляющих косинусов равны, в 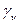.частности

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)