Параллельно включенных агрегатов: распределение нагрузок

Задача формулируется следующим образом (рис.9.1):

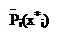
Рис. 9.1. Рис. 9.2.

– требуется выбрать нагрузку каждого из агрегатов и состав работающих агрегатов, включённых параллельно, если общая нагрузка (суммарный расход сырья) задана, а общая производительность должна быть максимальной.

С= ,

где X_i – нагрузка на каждый агрегат i=1,2…n, С – суммарная нагрузка,

Р= ,

где Р_i – производительнлсть i-го агрегата i=1,2…n, Р – суммарная производительность.

Для каждого из агрегатов известна нагрузочная характеристика – зависимость производительности P_i от расхода сырья X_i (рис. 9.2).

Тогда критерий оптимальности запишется в виде:

P = (X_i) ® max (9.20)

а ограничения X_i = 0 или X_i*£ X_i £ X_i^*.

Первое из этих условий относится к случаю, когда агрегат выключен, а второе – когда он работает. Эти условия удобно переписать, исключив слово «или», для чего вводится целочисленная переменная Vi.

Обозначив X_i = V_i , получаем критерий оптимальности

P = ® 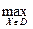(9.21)

V_i= , i=1…n (9.22)

D= (9.23)

Условие (9.23) соответствует выполнению требования суммарной нагрузки по сырью. Наличие целочисленных переменных значительно усложняет решение этой задачи. Рассмотрим некоторые варианты постановки задачи распределения.

Поиск по сайту: