Аналитический метод решения задачи

Аналитический метод использует необходимое условие max функции нескольких переменных:

Для того чтобы в точке функция , необходимо, чтобы (3.3), для всех i=1,2…n. Для выделения точек максимума необходимо также проверить знаки диагональных миноров матрицы вторых производных (матрицы Гессе).

В общем случае:

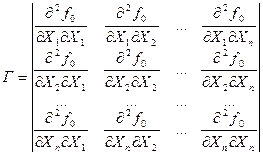(3.4)

Для функции двух переменных:

(3.5)

(3.6)

где - главный определитель матрицы.

В зависимости от знака D возможны три случая:

1) D < 0 – экстремум отсутствует, точка перегиба,

2) D = 0 – требуется дополнительное исследование,

3) D > 0 – экстремум есть, причем в случае

< 0 и 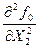< 0, это max, а при

> 0 и 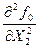> 0 – min.

Пример.

Определить максимум функции

;

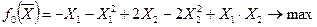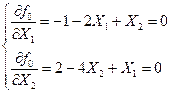
Откуда ,

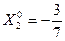
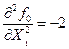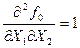
< 0

< 0 ,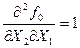

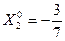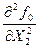откуда > 0, т.е. , - точка max, т.к. < 0 и < 0.

Поиск по сайту: