Метод направленного перебора

Данный метод аналогичен методу равномерного поиска для функции одной переменной.

Делим области допустимых значений и 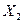на равные отрезки таким образом, чтобы количество отрезков по обеим осям было равно , где - величина допустимой погрешности. . Проведя перпендикуляры к осям во всех выделенных точках, получаем сетку на плоскости X₁, X₂ с количеством узлов (рис. 3.4). Вычисляем значения во всех узлах (рис. 3.4.). Сравниваем полученные значения и за решение принимаем координаты узла с наибольшим значением целевой функции .

Рис. 3.4.

Чем меньше шаг сетки, тем точнее результат, но и выше трудоемкость. На практике данный метод применяется только для вычисления глобального максимума невыпуклых функций.

Все остальные применяемые на практике методы, представляют собой итерационные многошаговые процедуры, в которых на каждом шаге расчета должно получаться большее значение целевой функции, чем на предыдущем.

Каждый метод включает в себя:

1) правило перехода от одного шага к другому,

2) правило остановки расчета.

В зависимости от правила перехода численные методы делятся на:

1. методы нулевого порядка, в которых правило перехода требует вычисления только самой целевой функции,

2. методы первого порядка (градиентные методы) в которых требуется вычисление первых частных производных целевой функции,

3. методы второго порядка – требуют вычисления вторых частных производных целевой функции.

Ниже будут рассмотрены только методы нулевого и первого порядков, т.к. в задачах оптимизации с возможными неточностями в исходных данных и с функциями, заданными алгоритмически, характерными для оптимизации технологических процессов, вычисление матрицы вторых производных приводит к значительным ошибкам и методы второго порядка не находят применения.

Поиск по сайту: