АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Принцип максимума Понтрягина

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. ERP-стандарты и Стандарты Качества как инструменты реализации принципа «Непрерывного улучшения»
  3. I Психологические принципы, задачи и функции социальной работы
  4. I. Сестринский процесс при гипертонической болезни: определение, этиология, клиника. Принципы лечения и уход за пациентами, профилактика.
  5. I. Сестринский процесс при диффузном токсическом зобе: определение, этиология, патогенез, клиника. Принципы лечения и ухода за пациентами
  6. I. Сестринский процесс при остром лейкозе. Определение, этиология, клиника, картина крови. Принципы лечения и ухода за пациентами.
  7. I. Сестринский процесс при пневмонии. Определение, этиология, патогенез, клиника. Принципы лечения и ухода за пациентом.
  8. I. Сестринский процесс при хроническом бронхите: определение, этиология, клиника. Принципы лечения и уход за пациентами.
  9. I. Сестринский процесс при хроническом гепатите: определение, этиология клиника. Принципы лечения и ухода за пациентами. Роль м/с в профилактике гепатитов.
  10. I. Структурные принципы
  11. II. Принципы процесса
  12. II. Принципы средневековой философии.

(7.11)

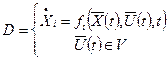i = 1, 2, …, n. (7.12)

Для решения задачи (7.11), (7.12) используется необходимые условия оптимальности, известные как принцип максимума Понтрягина. Составляем функционал Понтрягина:

(7.13)

Если и 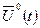решение задачи (7.11), (7.12), то найдется такой вектор 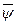, что при и 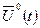функция Н достигает максимум по

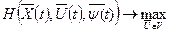(7.14)

Составляющие вектора 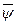являются решением системы дифференциальных уравнений.

(7.15)

с граничным условием 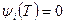, (7.16)

если не заданы составляющие при t=T. Если условия заданы в общем виде

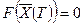, (7.17)

то 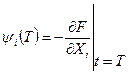(7.18)

Последовательность решения задачи (7.11) (7.12)

1) Составляем функционал Н в соответствии с (7.13) и из условия (7.14) определяем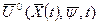

2) Решаем систему уравнений (7.15) для переменных 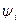с граничными условиями (7.16) или (7.18).

3) Решаем систему дифференциальных уравнений (7.12) совместное решение позволяет найти .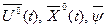

 

8. Оптимальное управление технологическими процессами.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)