АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод градиента

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.2. Двойственный симплекс-метод.
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. Метод рассмотрения остатков от деления.
  8. I. Методические основы
  9. I. Методические основы оценки эффективности инвестиционных проектов
  10. I. Организационно-методический раздел
  11. I. Предмет и метод теоретической экономики
  12. I. Что изучает экономика. Предмет и метод экономики.

Метод градиента – это пошаговая процедура поиска max целевой функции , в которой каждый шаг поиска выполняется в направлении градиента, исходящего из предыдущей точки. Координата очередной точки после К-го шага поиска определяется по формуле:

(3.8),

где -const, определяющая величину К-го шага.

Выбор производится, исходя из компромисса между скоростью поиска (растет при больших ) и точностью (растёт при малых ). Правильным считается такой выбор , при котором угол между направлениями вектора градиента в двух последовательных точках находится в пределах от 150 до 300. О величине угла удобно судить по cos этого угла, который вычисляют как отношение скалярного произведения градиентов и к произведению их модулей.

 

(3.9)

 

При 150 ≤ α ≤ 300 0,85 ≤ cos α ≤ 0,95 (3.10)

Расчет производится следующим образом:

 

1.Выбирается начальная точка (0) c координатами Xi (0), i =1,2… n.

2. Производится расчет проекций вектора градиента в начальной точке .

3.Выбирается γ и по формуле (3.8) определяются координаты следующей точки (1).

4.Производится расчет проекций вектора градиента в точке (1).

5.По формуле (3.9) определяется cos α.

6.Если условие (3.10) выполняется, то проводится расчет по пунктам 3-5 для точек (1) и (2) и т. д. Если (3.10) не выполняется, то величина γ корректируется и повторяется расчет по пунктам 3-5 для точек (0) и (1).

Остановка алгоритма производится при равенстве с заданной точностью нулю вектора градиента или или задается количество шагов N и за решение принимается последняя полученная точка (N).

Как видно из изложенного алгоритма, расчет достаточно громоздкий, причем заранее неизвестно, сколько раз придется рассчитывать один и тот же шаг. Мало того, что не определены критерии первоначального выбора коэффициента шага , но и нет гарантии, что повторный расчет будет удачным и не придется пересчитывать тот же самый шаг еще несколько раз. Действительно, после первого неудачного расчета шага мы получаем информацию только о том нужно ли уменьшить шаг (в случае , т.е. ) или увеличить (, т.е. 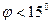), но насколько надо изменить шаг, чтобы второй расчет оказался стопроцентно удачным, неизвестно. Этих недостатков лишен метод крутого восхождения.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (4.433 сек.)