 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема Куна-Таккера
Применяется при решении полной задачи нелинейного программирования (4.1.) – (4.4.).
Если 
- вектор, являющийся решением задачи (4.1.) – (4.4.), то найдется вектор λ = (λ1,λ2,…λm), где m – число уравнений связи (4.3) и вектор
μ = (μ1,μ2,…μr), где r - число функциональных ограничений (4.4.) одновременно не равные нулю, такие что при 
, расширенная функция Лагранжа:
(4.19)
достигает 
по 
и min по 
При этом необходимо выполнение дополнительных условий
μk ≥ 0 (4.20)
μk ψk(
) = 0 (4.21)
Таким образом, необходимые условия оптимальности из теоремы Куна-Таккера:
(4.22)
(4.23)
Если автономные ограничения отсутствуют, тогда знак вариации варьируемых переменных 
не определен и условие (4.22) преобразуется в условие:
(4.24)
Пример: Определить 
при
D= X1 + X2 = 0
X1 – 1 ≥ 0
Составляем расширенную функцию Лагранжа:
≥ 0;
Автономные ограничения отсутствуют, поэтому используем необходимые условия оптимальности (4.24) и (4.23)
=-2 
+2+ + =0
+ = 0
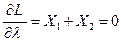
Так как мы получили систему из трех уравнений с четырьмя неизвестными 
, то для решения задачи необходимо использовать дополнительные условия (4.20) и (4.22). Эти условия в рассматриваемой задаче будут выполняться в двух случаях:
1). μ = 0; ψ(X) = X 1 – 1 ≥ 0, тогда имеем:
-2 X 1 + = - 2 X 1 – X 2 = 1 
= 0.5
-2 X 2 + = 0, откуда X 1 + X 2 = 0, 
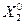= - 0.5
X 1 + X 2 = 0
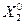При полученных значениях и условие X 1 - 1 ≥ 0 не выполняется, следовательно, принятое допущение некорректно.
Заметим также, что в случае μ = 0, расширенная функция Лагранжа (4. 19) превращается в обычную функцию Лагранжа (4. 6), которая составляется в случае отсутствия функциональных ограничений (4. 4), что не соответствует условиям рассматриваемого примера.
2). µ > 0; X 1 – 1 = 0; следовательно: X 1 = 1
Необходимые условия оптимальности:
-2 X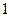 
+ λ + μ = -2
-2 X 2 + λ = 0
X 1 + X 2 = 0
Откуда, с учетом X 1= 1, получаем X 2= -1; λ = -2; μ = 2 > 0, следовательно, условие (4. 20) выполняется.
Таким образом, задача решена X 10 = 1, X 20 = -1.
Очевидно, что наложение на область допустимых решений D дополнительных условий уменьшает значение получаемого максимума функции f 0.
Для подтверждения этого положения найдем для рассмотренного примера максимальные значения целевой функции в отсутствии ограничений (безусловный максимум), при наличии одного ограничения типа связи и при наличии обоих ограничений, предусмотренных в условии примера.
1. Необходимые условия оптимальности целевой функции в отсутствие ограничений
; где M1 – безусловный 
2. Это случай μ = 0, т.е. отсутствуют функциональные ограничения. Решения для него получены выше.
M2 = max f0 (Х) = – (0.5)2 – (0.5)2 + 2 · 0.2 = 0.5
X€D
D: X1+X2=0
3. При наличии обоих ограничений выше получено 
M3 = max f0 (X) = - (1)2 – (-1)2 + 2 · 1 = 0
X€D
 |
D= X1+X2=0
X1 -1 ≥ 0
M1 > M2 > M3 - что и требовалось доказать.
Поиск по сайту: