Метод неопределенных множителей Лагранжа

Метод неопределенных множителей Лагранжа применяется при решении неполной задачи (4.1) – (4.3), то есть в случае, когда в условиях задачи отсутствуют функциональные ограничения (4. 4).

Исходная задача (4.1.) – (4.3.) заменяется задачей определения безусловного max функции Лагранжа, которая конструируется следующим образом (для m = 1, то есть при наличии одного ограничения типа связи (4.3.)),

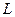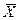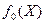(λ, ) = + λ ּ 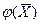→ 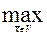(4.6.)

где: λ = const - неопределенный множитель Лагранжа.

Такая структура функции L обеспечивает ее совпадение с функцией 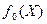при условии 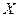€ D, так как в этом случае 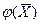= 0

Из выражения (4.5.) следует, что

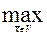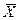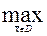
L (λ, ) 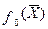(4.7.)

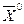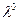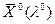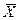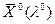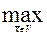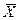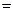
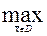
Допустим, что найдены значения и , которые обеспечивают безусловный максимум функции Лагранжа, т.е. =argmax L (λ, ). Если принадлежит области D, тогда L (λ, ) 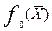, а при всех

других λ соотношение (4.7) выполняется как чистое неравенство. Следовательно в точке решения задачи условного max(4.1.) – (4.3.) функция Лагранжа достигает max по вектору Xи min по λ, то есть решением задачи условного maxявляется седловая (от слова седло) точка функции Лагранжа (рис. 4.2.).

На рис. 4.2 представлены три сечения функции L , взятые при трех различных значенияхλ.

Рис4.2

Решением задачи являются значенияX⁰ иλ⁰, обеспечивающие максимум функции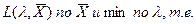

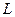
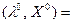
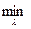
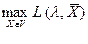(4.8.)

Для выполнения условия (4.8) необходимо, чтобы первые частные производные функции Лагранжа по Х_i и по l были равны нулю, т.е.

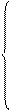
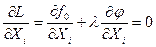(4.9)

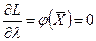(4.10)

Таким образом, выражения (4.9), (4.10) являются необходимыми условиями для нахождения точки условного максимума исходной целевой функции ¦₀(Х).

Этот результат распространяется и на случай m > 1, то есть количество уравнений связи больше одного.

(4.11)

Рассмотрим в качестве примера пример 3 из раздела 1.2 (распределение нагрузок между параллельно включенными агрегатами), введя обозначения:

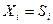- потребление сырья i–ым агрегатом;

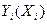- производительность i– го агрегата;

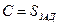- заданная суммарная нагрузка по сырью.

Для упрощения примем 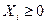, т.е. сначала рассмотрим случай, когда на переменные накладываются автономные ограничения, требующие чтобы нагрузки на агрегаты были положительны, т.е. физически реализуемы.

Тогда получаем:

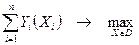
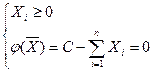
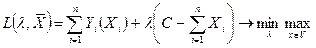(4.12)

Дифференцируя (4.12) получаем необходимые условия оптимальности

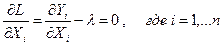(4.13)

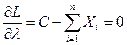(4.14)

Задача может решаться графически (рис 4.3).

Для этого на графиках зависимости 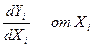(рис. 4.3 б) полученных путем графического дифференцирования нагрузочных характеристик Y_i (X_i) (рис. 4.3 а) находится такая прямая, параллельная оси ОХ, сумма проекций точек пересечения которой с этими графиками равна 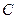, т.е. решением задачи являются такие значения 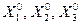, при которых выполняется условие 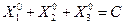, что необходимо, для выполнения условия (4.14). При этом по оси ординат определяется значение 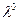, в соответствии с выражением (4.13).

Если характеристики 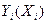выпуклы вверх, то эта задача имеет единственное решение.

Для подобных задач действует правило равных приростов: при оптимальном распределении нагрузок 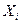производные 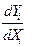для всех агрегатов должны быть одинаковы.

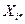
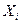
В реальных задачах обычно присутствуют автономные ограничения на нагрузки вида 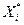(4.15), т.е. для практически любого технологического аппарата на допускается как перегрузка, так и работа вхолостую.

В этом случае задача решается следующим способом:

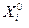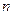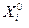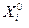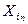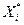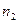Рассчитывают по правилу равных приростов. Если все они удовлетворяют условию (4.15), задача решена. Иначе, если среди значений , есть значение = > и значений 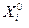= 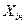< 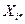то алгоритм распределения следующий.

Рассчитывают:

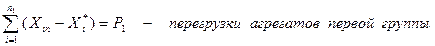
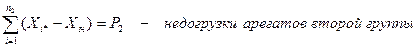
Здесь возможны три варианта:

1). 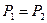. Тогда для оптимального распределения нагрузок необходимо все n₁ агрегатов 1-й группы загрузить до 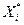, а все n₂ агрегатов 2-ой группы до 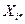, остальные агрегаты до 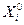, рассчитанного по правилу равных приростов.

2). 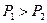_. Необходимо все n₁ агрегатов 1- ой группы загрузить до ,

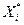рассчитать величину и решить задачу условной оптимизации для остальных (n-n₁) агрегатов:

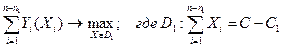
3) 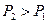_. Все n₂ агрегатов 2-ой группы загружаются до 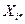, рассчитывается 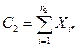и решается задача условной оптимизации для остальных (n-n₂) агрегатов:

Частный случай распределения сырья для линейных характеристик вида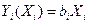

Заметим, что чисто линейных нагрузочных характеристик, при которых производительность аппаратов прямо пропорциональна их нагрузке на всем диапазоне ее возможных значений, не существует. Однако любая нагрузочная характеристика имеет практически линейный участок (см. рис. 4.3 а) и возможны режимы работы, предусматривающие функционирование аппаратов в диапазоне нагрузок, соответствующих именно таким участкам.

В этом случае правило распределения следующее:

1). Ранжируем (расставляем) аппараты в соответствии с правилом 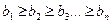, т.е. располагаем в порядке убывания производных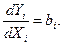

2). Назначаем 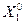= 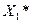, вычисляем 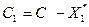и проверяем условие .

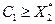3). Если оно выполняется, то 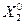= иначе = .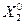

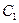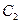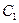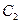Вычисляем = – , если ≥ , то 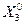= 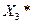, иначе 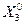= 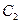и т.д.

Покажем экономический смысл множителей Лагранжа, для чего рассмотрим аналогичную задачу:

Распределить ограниченное количество сырья С между n потребителями, выпускающими из него готовый продукт, так, чтобы обеспечить максимальный суммарный доход владельца сырья и его потребителей.

Обозначим 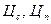- цена сырья и продукта,

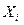- количество сырья, полученное i -м потребителем,

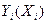- количество продукта, изготовленное i-м потребителем.

Тогда доход 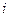-го потребителя:

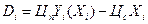(4.16)

а общий суммарный доход владельца сырья и всех потребителей, который будем оптимизировать:

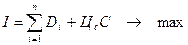(4.17)

Подставляя (4.16) в (4.17), получаем:

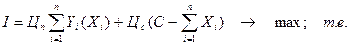
(4.18)

Сравнивая (4.18) и (4.12) получаем - множитель Лагранжа

показывает равновесную, оптимальную с точки зрения поставленной задачи, цену сырья, Ц_с, при постоянной цене продукта Ц_n, или наоборот.

Поиск по сайту: