Пример. Так как в данном случае n=3, то выражение (5.16) имеет вид

Так как в данном случае n=3, то выражение (5.16) имеет вид

Составляем функцию Беллмана для последнего, т.е. третьего этапа

Для обеспечения max (X₂ + U₃) необходимо, чтобы

Так как , то вышеуказанное условие будет выполняться только при ∆ U₃ < 0, т.е. на верхней границе управления U₃⁰ = 1.

Следовательно, B₃(X₂)=X₂+1. Эти же рассуждения, как показано ниже, справедливы и для расчета U2 и U1.

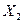
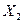
Так как , то необходимо выполнение условия , т.е. - верхняя граница управления, откуда следует:

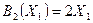+4

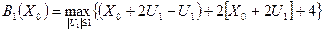, т.к. по условию задачи , то

,

Так как , то необходимо ΔU₁<0, т. е. U₁⁰=1 – верхняя граница управления.

; ; ;

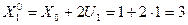Таким образом, задача решена.

Поиск по сайту: