 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Постановка задачи на примере и ее формализация
Рассмотрим технологическую схему получения ректифицированного спирта, представленную на рис. 5.1.
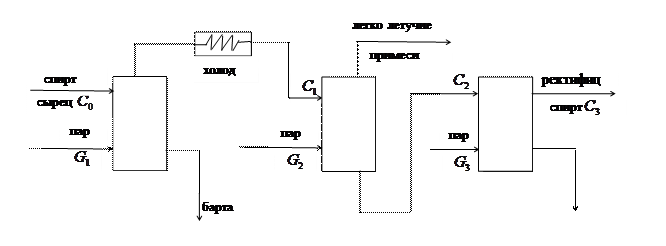
Рис 5.1.
С 0, С 1, С 2, С 3 - концентрации спирта;
G 1, G 2, G 3 - расходы пара;
C 1= F 1 (C 0, G 1); C 2= F 2 (C1,G2); C 3= F3 (C2,G3);
где F 1, F 2, F3 функции, связывающие выход и вход на каждой стадии ректификации.
Необходимо минимизировать расход пара, т.е. найти такие
G 10, G 20, G 30, при которых
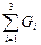→ min
Учитывая, что argmax f0(X) = argmin (-f0(X)), (см. раздел 1.4.), получаем оптимизационную задачу для многостадийного процесса.
- → 
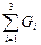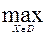
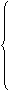Gi* ≤ Gi ≤ Gi * i = 1, 2, 3
D= Ci - Fi (C i-1, Gi) = 0
C3 ≥ Cзад
Формализуя данную задачу для процесса из n стадий, получаем структурную схему, представленную на рис. 5.2., для каждого элемента которой выполняется условие Xi = fi (Xi -1, Ui) и формируется целевая функция f0i (Xi, Ui) (в примере Gi).
Рис. 5.2
Где,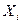 
- переменные состояния (в примере Ci)
- переменные управления (в примере Gi)
Для всего процесса получаем:
I = 
(
) → 
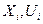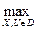, (5.1.)
где n – количество стадий (этапов) процессов.
|
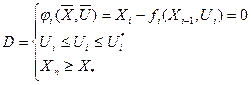
Последовательность управлений U1, U2…Un(см. рис. 5.2) называется стратегией управления.
Оптимизация многостадийных процессов сводится к отысканию оптимальной стратегии управления, которая обеспечит перевод процесса из заданного начального состояния X0 в заданное конечное состояние Xn с минимальными затратами на управление.
5.2. Решение задачи методом неопределенных множителей Лагранжа.
Оптимизационная задача (5.1.) – (5.4.) представляет собой задачу определения условного max с автономными ограничениями (5.3), (5.4) и ограничениями типа связи (5.2). Как известно (см. раздел 4.2.1.) такая задача может быть решена методом неопределенных множителей Лагранжа:
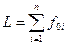(Xi, Ui)+ 
Необходимые условия оптимальности
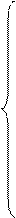
(5.6.)
D= 
(5.7.)
= Xi - fi (Xi -1, Ui) = 0 (5.8.)
Поясним вывод выражения (5.6.). Например, для n = 2 имеем:
L = f 01(X 1 U 1) + f 02(X 2 U 2) +λ1 (X 1- f 1(X 0 U 1)) +λ2 (X 2– f 2(X 1 U 2))
Произведя замену для случая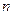 
стадий 
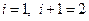, получаем выражение (5.6), которое является рекуррентной формулой для расчета λ i. через λi+1.
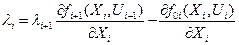(5.9.)
Для его использования задается граничное условие. Очевидно, что после окончания процесса
λ n+1 = 0 (5.10.)
Пример:
Из условия примера следует:
Вычисляем значения частных производных, содержащихся в правой части выражения (5.9.).
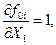
для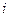 
=1, 2, 3
Составляем функцию Лагранжа аналогично (5.5.):
(Xi, Ui)+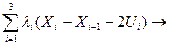 
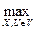
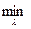
Из выражения (5.10) для случая n=3 имеем:
λn+1= λ4= 0
По выражению (5.9) вычисляем λi (i =1,2,3), используя значения частных производных, вычисленные выше
λ2 = λ3ּ1 - 1 = (-1) ּ1 - 1 = - 2
λ1 = (- 2) ּ1 – 1 = - 3
Проверяем выполняемость условия (5.7)
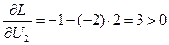
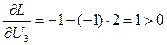
Так как производные 
, (i =1,2, 3) больше нуля, то необходимое условие оптимальности (5.7) может быть выполнено только при ∆ Ui < 0, т.е. при верхнем граничном значении управления (см. раздел 1.4.), следовательно, U 10= U 20= U 30=1.
Зная оптимальные значения переменных управления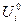 
, (i =1,2, 3), рассчитываем оптимальные значения переменных состояния Xi 0по уравнению связи (5.8).
X 10 = X 0+ 2 U 1 = 1 + 2 · 1 = 3
X 20 = 3 + 2 · 1 = 5
X 30 = 5 + 2 · 1 = 7
Вычисляем максимальное значение критерия оптимальности
= (3 – 1) + (5 – 1) + (7 – 1) = 12
Задача решена.
Поиск по сайту: