Постановка задачи. Методы решения оптимизационных задач

В данном случае в критерии оптимальности присутствует только одна варьируемая переменная. На нее могут быть наложены только автономные ограничения и постановка задачи принимает вид:

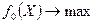(2.1)

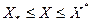(2.2)

В соответствии с теоремой Вейерштрассе всякая функция 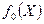, непрерывная на замкнутом и ограниченном множестве (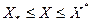), достигает на нем своего наибольшего и наименьшего значения. Функция 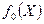выпукла на 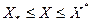, если она имеет на этом множестве единственный максимум. Выпуклая функция обладает тем свойством, что, если через две любые принадлежащие ей точки провести прямую (с координатами и 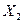), то любая промежуточная точка этой прямой не будет превышать значение функции при том же Х (рис.2.1 ). Для выпуклой функции справедливо выражение:

, где

Если функция не выпукла (неунимодальна), то она будет иметь несколько точек максимума, причем значение функции в этих точках будет различным (рис. 2.2)

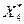В этом случае точка, соответствующая наибольшему значению функции (точка на рисунке) называется точкой глобального максимума, а остальные точки (, , , ) – локальными максимумами функции.

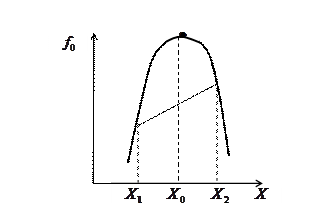
Рис.2.1

Все методы решения оптимизационных задач, в том числе методы определения максимума функции одной переменной делятся на:

1. Аналитические, основанные на необходимых или достаточных условиях оптимальности, причем достаточные условия применяются только в случае сложноорганизованных областей допустимых значений D.

2. Численные, которые представляют собой вычислительную процедуру, обеспечивающую последовательное уточнение решения от некоторого начального приближения до максимума с заданной допустимой погрешностью.

Поиск по сайту: