III. Краткая теоретическая часть

Дифракцией называется огибание волна­ми препятствий, соизмеримых с длиной волны, встречающихся на их пу­ти, или в более широком смысле — любое отклонение распространения волн от законов геометрической оптики вблизи любых неоднородностей (препятствий).

Явление дифракции можно наблюдать с помощью дифракционной решётки. Дифракционная решётка представляет собой стеклянную или ме­таллическую пластинку, на которой через строго одинаковые интервалы нанесены параллельные штрихи. В итоге получают последовательность параллельных щелей равной ширины а, разделенных непрозрачными промежутками равной ширины b. Величина d = a+b, называется периодом (постоянной) дифракционной решётки.

Пусть на дифракционную решетку падает нормально световой поток. Благодаря дифракции свет от щелей будет распространяться во всех направлениях (на рис. 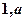показаны только два луча). Разность хода 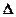параллельных лучей, дифрагирующих от щелей под углом j, равна:

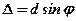, (1)

где j - угол дифракции, d – постоянная дифракционной решетки.

Собранные линзой в одну линию (проходящую параллельно щелям через точку В на экране) эти лучи интерферируют. Для того, чтобы в точке В наблюдался интерференционный максимум, разность хода 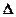между волнами, испущенными соседними щелями, должна быть равна целому числу длин волн (четному числу полуволн):

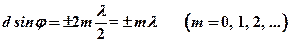, (2)

где m – порядок максимума, l - длина световой волны.

Таким образом, выражение (2) задает условие главных максимумов.

Очевидно, что в тех направлениях, в которых ни одна из щелей не распро­страняет свет, он не будет распростра­няться и при многих щелях, т.е. главные минимумы интенсивности (как и в случае одной щели) будут наблюдаться в направлениях, определяе­мых условием:

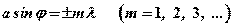, (3)

где а - ширина щели.

Если дифракционная решётка состоит из 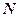щелей, то дополнительные минимумы интенсивности будут наблюдаться в направлениях, определяе­мых условием:

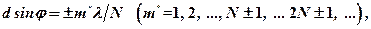(4)

где m ^* может принимать все целочислен­ные значения, кроме 0, N, 2N ,..., т. е. кро­ме тех значений, при которых условие (4) пере­ходит в (2). Следовательно, в случае N щелей между двумя главными максиму­мами располагается N─1 дополнитель­ных минимумов, разделенных сла­быми вторичными максимумами.

Чем больше щелей N, тем больше световой энергии пройдет че­рез решетку, тем больше минимумов образуется между соседними главными макси­мумами, тем, следовательно, более интен­сивными и более острыми будут главные максиму­мы.

При освещении дифракционной решётки белым светом на экране наблюдаются кроме светлой полосы (нулевого максимума) ещё и цветные линии, т.е. происходит разложение белого света в спектр. Цветные линии располагаются по обе стороны от нулевого максимума примерно на равных расстоя­ниях (рис.1, b), причем фиолетовая область спектра будет обра­щена к центру дифракционной картины, красная — наружу. Это следует из формулы (2) в которой угол отклонения увеличивается с увеличением длины волны, т.е. j ~ l.

В настоящей работе постоянная дифракционной решётки d известна (она указана на решётке). Порядок спект­ральной линии m задается преподавателем. Для определения длины волны света l из фор­мулы (2), соответствующей наблюдаемому дифракционному максимуму, надо знать sinj.

В спектре (рис. 1, b) угол отклонения фиолетовых лучей определится так: 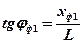, (5)

где x_ф1 - расстояние от максимума нулевого порядка (m=0) до фиолетовой линии в спектре первого порядка (m=1), L - расстояние от дифракционной решётки до экрана.

Используя соотношение (2), определим:

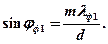(6)

В нашем случае углы дифракции малы (j < 7^о) и можно считать 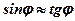и тогда приравнивая (5) и (6) для любого цвета и порядка спектра можно записать:

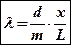, (7)

где l – длина световой волны, d – постоянная дифракционной решетки, x – расстояние от максимума нулевого порядка (m =0) до линии в спектре m-го порядка. L – расстояние от дифракционной решётки до экрана.

Основными характеристиками дифракционной решётки являются дисперсия и разрешающая способность.

Угловая дисперсия D определяется угловым расстоянием между двумя спектральными линиями, отнесённым к разности их длин волн :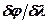

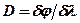
Значение дисперсии получаем, дифференцируя формулу (2):

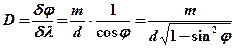, т.е.

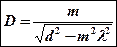, (8)

где D ─угловая дисперсия, l ─длина световой волны, m ─ порядок спектра, d ─постоянная дифракционной решетки.

Дисперсия возрастает с увеличением порядка спектра.

Разрешающая способность 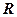характеризует минимальную разность длин волн dl, которые в спектре видны раздельно, т.е.

.

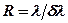Можно показать, что для дифракционной решетки

,

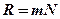где m ─ порядок спектра; N ─ общее число штрихов решётки.

 

Таким образом:

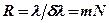. (9)

 

Измерив ширину освещенной части решётки l, найдём число штрихов решётки N в этой части:

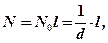(10)

где 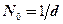─ число штрихов на единице длины решётки, d ─ постоянная дифракционной решётки.

 

Таким образом, из соотношений (9) и (10) разрешающая способность дифракционной решётки определится по формуле:

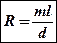, (11)

где l – ширина освещённой части решётки, d- период решётки, 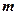- порядок спектра.

Разность 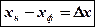(12)

определяет длину спектра любого порядка на экране.

Воспользовавшись соотношением (2) можно рассчитать номер последнего дифракци­онного максимума, который можно было бы наблюдать при определен­ных условиях на экране с помощью используемой дифракционной решётки:

 

 

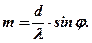
Поскольку синус не может быть больше единицы, т.е. 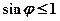, получаем, что 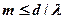, следовательно

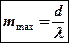. (13)

IV. Экспериментальная часть.

 

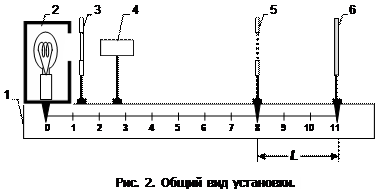1 - оптическая скамья; 2 - осветитель; 3 - щелевая диафрагма;

4 - объектив для получения резкого изображения дифракционной картины; 5 - дифракционная решётка; 6 - матовый экран.

 

Задание 1. Нахождение длины световой волны.

1. Перемещая рамку с дифракционной решёткой 5, установить по

заданию преподавателя расстояние L между дифракционной

решёткой и экраном 6 (положение экрана не изменять!!! ).

2. Измерить расстояние от центральной полосы до красной слева

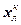() и справа (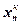). Результаты измерений занести в таблицу 1.

Аналогичные измерения провести для зеленых полос (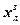 и )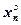

и фиолетовых (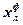 и 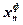) полос 1-го порядка (m = 1).

3. Определить средние значения , _,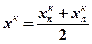

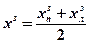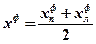для красного, зеленого и фиолетового цветов.

4. Повторить пункты 1-3 не менее 5 раз, изменяя расстояние

между решеткой и экраном (L =100, 150, 200, 250, 300 мм).

5. Вычислить длины волн наблюдаемых спектральных линий

(красной, зелёной и фиолетовой) по формуле (7) и занести

результаты в таблицу 2.

6. По заданию преподавателя можно выполнить пункты 2-5 для

спектров более высокого порядка (например, m = 2).

Задание 2. Определение характеристик решётки.

1. Измерить освещенную ширину решетки (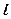) для L =300мм.

2. Используя соотношение (8), вычислить угловую дисперсию для

красного, зеленого и фиолетового цветов для данного .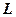

3. Используя соотношение (11), определить разрешающую

способность дифракционной решётки и занести

результаты в таблицу 2.

Задание 3. Определение характеристик спектра.

1. Используя соотношение (13), рассчитать для всех длин волн

номер последнего дифракционного максимума m _max и занести

результаты в таблицу 2.

2. Используя соотношение (12), рассчитать длину спектра 1-го

порядка.

Таблица 1.

№/№ п/п	L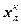
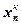
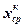
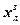
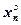
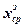
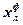
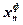
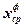
мм	мм	мм	мм	мм	мм	мм	мм	мм	мм

 

Таблица 2.

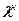
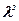
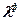
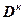
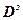
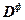
№/№ п/п	L							R	mmax
мм	мм	мм	мм	рад/м	рад/м	рад/м
Среднее значение
Абсол. погрешн.
Относ. погрешн.

 

Контрольные вопросы.

1. В чем проявляется явление дифракции света?

2. В чем состоит принцип Гюйгенса-Френеля? Какое дополнение в принцип Гюйгенса ввел Френель?

3. В каком направлении световая энергия, излучаемая вторичными источниками, максимальна?

4. Напишите математическое выражение условия, при которых будут наблюдаться минимумы и максимумы дифракции от дифракционной решетки.

5. Что такое период (постоянная) дифракционной решетки?

6. На что и как влияет изменение величины постоянной дифракционной решетки?

7. Как располагаются цветные линии в дифракционном спектре?

8. Почему при использовании белого света только центральный максимум белый, а боковые максимумы радужно окрашены?

9. Какими параметрами характеризуется дифракционная решетка в качестве спектрального прибора?

10. Дать понятия дисперсии и разрешающей способности дифракционной решётки.

 

Поиск по сайту:

---