АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Основные величины, характеризующие движение жидкости или газа. Линейная и объёмная скорости; соотношение между ними

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. D) постоянных затрат к разнице между ценой реализации продукции и удельными переменными затратами.
  3. E) Для фиксированного предложения денег количественное уравнение отражает прямую взаимосвязь между уровнем цен Р и выпуском продукции Y.
  4. I Раздел 1. Международные яиившжоши. «пююеям как процесс...
  5. I. IIонятие, виды и соотношение источников МЧП.
  6. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  7. I. Линейная алгебра
  8. I. О различии между чистым и эмпирическим познанием
  9. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  10. I. ОСНОВНЫЕ СПОСОБЫ ПЕРЕДВИЖЕНИЯ И ПРЕОДОЛЕНИЯ ПРЕПЯТСТВИЙ
  11. I. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
  12. I. Основные термины и предпосылки

Основной характеристикой любого движения является его скорость. В случае течения жидкости (или газа) термин „скорость“ применяется в двух смыслах. Скорость перемещения самих частиц жидкости (или плывущих вместе с жидкостью мелких тел – например, эритроцитов в крови) обозначают υ и называют линейной скоростью.

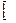м/с [1],

где х – координата частицы (при равномерном движении можно написать 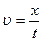). Однако, на практике чаще важнее знать объём V жидкости, протекающей через поперечное сечение данного потока (трубы, русла реки, кровеносного сосуда и т.п.) за единицу времени. Эту величину называют объёмной скоростью и обозначают Q.

Q = 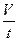(2)

В физиологии и медицине врача большей частью интересует именно объёмная скорость Q. Например, чтобы оценить, достаточно ли кислорода получает головной мозг (что очень важно при многих заболеваниях), надо знать объёмную скорость кровотока в артериях, снабжающих кровью мозг. Аналогично, для оценки дыхания необходимо оценить объём воздуха, поступающего по трахее за единицу времени, то есть опять-таки объёмную скорость. При заболеваниях почек и при гипертонической болезни крайне важна оценка объёмной скорости кровотока в почечной артерии. Можно привести много других примеров.

Между линейной скоростью υ и объёмной скоростью Q существует простая связь. Рассмотрим трубку с площадью поперечного сечения S (см. Рис. 2).

 

1 2

S 1 V

х

Рис. 2.

Выделим поперечный слой жидкости, который в момент времени t = 0 занимает положение 1. Через некоторое время t он переместится в положение 2, отстоящее на расстояние x = υ·t. При этом через трубку пройдёт объём жидкости V = S·x. Объёмная скорость жидкости Q при этом будет равна 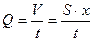. Но , поэтому

Q = S ·υ (3)

Если течение стационарно, то

Q = S1·u1 = S2.u2 = S3.u3 = ……. = const (4)

Это уравнение неразрывности струи.

Таким образом, если мы имеем дело с жесткой неразрывной трубой переменного сечения, то линейная скорость течения жидкости тем больше, чем меньше сечение трубы.

На основании уравнения неразрывности струи можно качественно объяснить изменения скорости течения крови в системе кровообращения. Самым узким сечением в большом круге кровообращения обладает аорта (S ≈ 4 см2). По мере ветвления артериальных сосудов суммарная площадь их сечения увеличивается. Наибольшая суммарная площадь поперечного сечения приходится на уровень капилляров (≈ 11000 см2, хотя обычно кровь течет всего через 3000 см2, а остальные капилляры находятся в спавшемся состоянии). Следовательно, в большом круге кровообращения площадь суммарного просвета капилляров, в которых есть кровоток, в 700-800 раз больше поперечного сечения аорты. С учетом уравнения неразрывности струи это означает, что линейная скорость кровотока в капиллярах в 700-800 раз меньше чем в аорте (около 1 мм/с и 0,5-1 м/с, соответственно).


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)