Течение идеальной жидкости. Теорема Бернулли

Идеальная жидкость – жидкость несжимаемая и не имеющая внутреннего трения (вязкости). Следовательно, при движении жидкости не происходит диссипации энергии (перехода механической энергии в тепло). Считалось, что таких жидкостей не существует, но в 1938 году академик П.Л.Капица обнаружил, что при температурах, очень близких к абсолютному нулю, подобными свойствами обладает жидкий гелий (Капица назвал такое поведение гелия «сверхтекучестью»; за открытие и исследование этого явления ему в дальнейшем была присуждена Нобелевская премия).

Хотя во всех остальных случаях движение жидкости обязательно сопровождается диссипацией энергии, понятие идеальной жидкости (как, например, и понятие идеального газа) имеет большое практическое значение, потому что во многих случаях формулы, выведенные для идеальной жидкости, можно без больших ошибок применять для движения реальных жидкостей и газов. Наиболее интересным примером является теорема Бернулли, полученная в начале XVIII века петербургским академиком Д.Бернулли. (Любопытно, что в Академии наук и в Петербургском университете он занимал кафедру физиологии, и интерес к проблемам движения жидкостей возник у него под влиянием исследований кровообращения).

Теорему Бернулли можно вывести таким образом. Поскольку при движении идеальной жидкости не происходит диссипации энергии, то ее полная механическая энергия постоянна. Если жидкость движется под действием внешнего давления, то ее полная энергия есть сумма кинетической энергии, потенциальной энергии силы тяжести и потенциальной энергии давления.

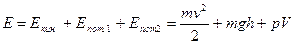(5)

Для идеальной жидкости Е= const.

.

Разделим на объем жидкости V; так как жидкость несжимаема, V = const.

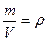, - плотность жидкости.

(6)

Это уравнение (теорема) Бернулли: В потоке идеальной жидкости сумма статического, гидростатического и гидродинамического давлений есть величина постоянная.

р – внешнее статическое давление, которое, согласно закону Паскаля, передается жидкостью во все стороны без изменения. 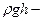давление силы тяжести жидкости, или гидростатическое давление. - давление, создаваемое вследствие движения жидкости - динамическое давление, направленное по вектору скорости жидкости.

Для горизонтального течения жидкости, когда =const, можно уравнение Бернулли упростить: .

Статическое давление - это то давление, которое движущаяся жидкость оказывает на стенки трубки.

Его можно измерить, если плоскость отверстия трубки манометра расположить параллельно линиям тока жидкости (рисунок 3-а). Если же плоскость отверстия

Рис. 3

трубки манометра будет перпендикулярна линям тока (рис. 3-6), то манометр покажет полное д авление. При расположении манометра, как показано на рис. 3-в, мы будем измерять разность между полным и статическим давлениями, то есть динамическое давление.

При нормальном кровообращении, как нетрудно подсчитать, динамическое давление составляет всего 1%-3% от полного. Например, если линейная скоростькрови в аорте составляет около 0,7 метра в секунду, то

(плотность крови ≈ 1000 кг^.м ^–3 ). Полное давление крови в аорте (среднее) составляет около 120 мм ртутного столба. Учитывая, что 1 мм.рт.ст. = 133 Па, получаем, что полное давление равно 16^.10 ³ Па, то есть р_{динамич} ≈ 1,5%. Однако, при усиленной физической нагрузке, а также при некоторых заболеваниях динамическое давление заметно возрастает, и его необходимо учитывать.

Из теоремы Бернулли следует, что там, где скорость жидкости или газа больше, статическое давление меньше, и наоборот. Например, при увеличении расхода воды в водопроводе давление на стенки труб падает. При сильном ветре динамическое давление сильно возрастает (пропорционально квадрату скорости ветра), поэтому статическое давление над крышей значительно падает. Под крышей, где нет движения воздуха, статическое давление остаётся высоким; разность давлений срывает листы кровли вверх.

Теорема Бернулли имеет большое практическое значение. Особенно важна она для авиации, потому что именно она объясняет возникновение подъёмной силы самолёта. Плоскостям (крыльям) самолёта придают такой профиль, что скорость воздуха, обтекающего крыло по верхней стороне, заметно больше, чем обтекающего по нижней. Поэтому динамическое давление больше сверху крыла, чем снизу, а статическое, наоборот, больше снизу. Разность статических давлений и создаёт силу, направленную вверх, то есть подъёмную силу. Первым, кто на этой основе разработал теорию полёта, был выдающийся учёный и инженер Н.Е.Жуковский, работы которого до сих пор лежат в основе конструирования летательных аппаратов.

Как нетрудно подсчитать, при нормальном кровообращении динамическое давление крови составляет всего 1%~3% от полного. Например, в аорте линейная скорость крови около 0,7 метра в секунду, откуда

(плотность крови ~ 1000 кг^.м^-3). Полное давление крови в аорте (среднее) около 120 мм рт. ст. Учитывая, что 1 мм рт. ст. = 133 паскаля, получаем, что полное давление равно 16^.10³ Па, то есть Р_{динамич} ~ 1,5%. Однако, при усиленной физической нагрузке, а также при некоторых заболеваниях динамическое давление заметно возрастает, и его необходимо учитывать.

Поиск по сайту: