Ламинарное течение жидкости по трубке. Формула Пуазейля

Рассмотрим часто встречающийся случай ламинарного движения жидкости по трубке с круглым сечением под действием разности давлений на её концах. Впервые этот случай был исследован французским врачом и физиологом Пуазейлем при изучении движения крови по сосудам; в дальнейшем она получила широкое применение в физике и технике. Формула Пуазейля позволяет рассчитать объёмную скорость течения жидкости по известным значениям радиуса трубки г, её длины L, вязкости жидкости и разности давлений на концах трубки p₁ – р₂ (рис. 6 ).

P₁ P₂

L

Рис. 6

(Вывод формулы Пуазейля интересующиеся могут прочитать в учебнике А.Н.Ремизова, стр. 150-151).

Как и можно было ожидать, объёмная скорость прямо пропорциональна разности давлений и обратно пропорциональна вязкости. Обращает на себя внимание очень сильная зависимость объёмной скорости от радиуса: Q ~ г⁴. Пусть, например, r₁ =2r₂. Тогда

Через широкую трубку протечёт в 16 раз больше жидкости!

Интересно сравнить движение жидкости с электрическим током (движением электрических зарядов). Запишем формулу Пуазейля в таком виде:

р₁ – р₂ = , и сравним её с формулой закона Ома, написанной так: U₁ – U₂ = R^.I. Легко видеть, что между этими формулами существует аналогия. В первой формуле слева стои т причина течения жидкости -разность давлений, во второй - причина возникновения тока, то есть разность потенциалов. Справа в первой формуле стоит объёмная скорость, то есть количество жидкости, протекающее в единицу времени; во второй формуле - сила тока, то есть количество зарядов, протекающее в единицу времени. Очевидно, величина

имеет смысл сопротивления движению жидкости. Ее так и называют - гидродинамическое сопротивление. R_ГД =

Используя это обозначение, можно формулу Пуазейля записать в таком виде: p₁ – p₂ = R_ГД.Q или Q =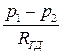

Рассмотренная аналогия имеет большое практическое значение. Так, при исследовании разветвлённых трубопроводов (например, водопроводной сети) можно пользоваться хорошо разработанными методами расчёта электрических цепей, в частности - формулами для последовательного и параллельного соединения проводников, которые верны и для гидродинамических сопротивлений.

Формула Пуазейля имеет большое значение при рассмотрении многих вопросов гемодинамики - раздела врачебной науки, изучающего движение крови по сердечно-сосудистой системе. Прежде всего, она объясняет распределение сопротивления между различными отделами кровеносной системы (в медицине его называют гемодинамическим сопротивлением). В аорте и крупных артериях с относительно большим диаметром гемодинамическое сопротивление невелико (несколько мм рт.ст.).По мере уменьшения радиуса сосудов гемодинамическое сопротивление возрастает, и наибольшим сопротивлением обладают самые мелкие артерии - артериолы. Радиус капилляров ещё меньше (примерно, в 2,5 раза), длина капилляра меньше, а вязкость крови в капиллярах больше. Если учесть всё это, то оказывается, что R_гд капилляра в 40-60 раз больше, чем у артериолы. Но каждая артериола снабжает кровью около 100 капилляров, соединённых параллельно. При этом общее сопротивление всех капилляров, отходящих от одной артериолы, будет равно R_к/n, где R_к - сопротивление одного капилляра, а n - число капилляров. Поэтому гемодинамическое сопротивление всех капилляров составляет 0,4 - 0,6 от R_гд артериол. (Разумеется, все цифры усреднённые; на самом деле в разных органах они могут быть различными, что можно учесть при более точных расчётах). Вены заметно шире артерий, поэтому гемодинамическое сопротивление венозного русла мало.

Таким образом, из всех участков кровеносной системы максимальным гемодинамическим сопротивлением обладают мелкие артерии и, особенно, - артериолы.

Так как разность давлений (падение давления) на участке, то есть величина р₁ – р₂, прямо пропорциональна гемодинамическому сопротивлению, наибольшее падение давления происходит именно в артериолах. Это имеет ключевое значение для регуляции кровяного давления. В стенках мелких артерий (и особенно – артериол) находится много мышечных волокон. Если артериальное кровяное давление (АКД) уменьшается, специальные рецепторы сигнализируют об этом нервным узлам, расположенным в стенках сосудов. Оттуда поступают нервные импульсы к мышечным волокнам артериол, волокна сокращаются, и диаметры артериол уменьшаются, В результате растёт гемодинамическое сопротивление и„ соответственно, повышается давление крови в крупных артериях. При увеличении АКД всё происходит в обратном порядке. Таким образом, у здорового человека АКД достаточно точно поддерживается постоянным.

Важно отметить, что во всех названных случаях диаметр артериол меняется относительно мало. Например, чтобы давление уменьшилось со 130 мм до 120 мм, достаточно увеличения диаметра артериолы в раз, или на 8%. Если наблюдать в микроскоп, то такое увеличение размера сосуда почти незаметно.

Заключение

Прослушав эту лекцию, Вы могли убедиться, что свойства жидкостей и особенности их движения во многом определяют протекание многих физиологических и патологических процессов. Некоторые явления, имеющие место в жидкостях, используются в широко распространённых методах диагностики и в лабораторных исследованиях. В ходе дальнейшего обучения Вы неоднократно будете сталкиваться с подобными примерами при изучении самых разных дисциплин (терапия, хирургия, гигиена, медицинская защита, физиология подводного плавания и аварийно-спасательного дела, авиационная медицина и др.).

«___» __________ 20__ г.

Исполнитель: Доцент Новикова Н.Г.

Поиск по сайту: