 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод последовательных уступок
Этот метод заключается в следующем: выбирают несколько противоречивых параметров, один из них назначают в качестве целевой функции, а для других последовательно принимаются конкретные значения. Задача оптимизации решается несколько раз при различных принятых значениях параметров. Этот метод рассмотрим на примере задачи, которая решалась в 2.2.
Алгоритм 2.3. Оптимизация методом последовательных уступок
1. Вызвать таблицу с условиями задачи (рис. 2.5).
| A | B | C | D | E | F | G | H | I | J | K | |
| Переменные | |||||||||||
| Имя | Прод1 | Прод2 | Прод3 | Прод4 | y1 | y2 | y3 | ||||
| Значение | |||||||||||
| Нижн.гр. | |||||||||||
| Верхн.гр. | |||||||||||
| Коэф.в ЦФ | |||||||||||
| Ограничения | |||||||||||
| Вид | Левая часть | Знак | Правая часть | ||||||||
| Трудовые | = | ||||||||||
| Сырье | = | ||||||||||
| Финансы | = |
Рис. 2.5
2. Принять параметры, по которым будем решать задачу.
Принимаем в качестве целевой функции прибыль, значения которой находятся в ячейке I6, а в качестве задаваемого параметра — величину неиспользуемых финансов уз, значение которой вводится в ячейку ввода исходных данных Н4.
В качестве первого значения вводим уз = 50.
3. Вызвать диалоговое окно Поиск решения.
4. Изменить граничные условия НЗ >= Н4 на НЗ = Н4.
5. Провести параметрический анализ, вводя на каждом шаге значения неиспользуемых финансов в ячейку Н4.
Результат параметрирования показан на рис. 2.6.
| A | B | C | D | E | F | G | H | |
| Итоговый сценарий | ||||||||
| Текущие значения: | Неисп. Фин=0 | Неисп. Фин=10 | Неисп. Фин=20 | Неисп. Фин=30 | ||||
| Изменяемые ячейки | ||||||||
| $B$3 | 0.00 | 10.00 | 11.67 | 13.33 | 15.00 | |||
| $C$3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |||
| $D$3 | 0.00 | 6.00 | 4.33 | 2.67 | 1.00 | |||
| $E$3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |||
| $F$3 | 16.00 | 0.00 | 0.00 | 0.00 | 0.00 | |||
| $G$3 | 110.00 | 26.00 | 22.67 | 19.33 | 16.00 | |||
| $H$3 | 100.00 | 0.00 | 10.00 | 20.00 | 30.00 | |||
| Ячейки результата | ||||||||
| $I$6 | ||||||||
| $I$9 | ||||||||
| $I$10 | ||||||||
| $I$11 | ||||||||
| Примечания: столбец «Текущие значения» представляет значения изменяемых ячеек в момент создания Итогового отчета по Сценарию. Изменяемые ячейки для каждого сценария выделены серым цветом. | ||||||||
| I | J | K | L | M | N | O | |
| Неисп.Фин=40 | Неисп.Фин=50 | Неисп.Фин=60 | Неисп.Фин=70 | Неисп.Фин=80 | Неисп.Фин=90 | Неисп.Фин=100 | |
| 15.00 | 12.50 | 10.00 | 7.50 | 5.00 | 2.50 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 1.00 | 3.50 | 6.00 | 8.50 | 11.00 | 13.50 | 16.00 | |
| 20.00 | 35.00 | 50.00 | 65.00 | 80.00 | 95.00 | 110.00 | |
| 40.00 | 50.00 | 60.00 | 70.00 | 80.00 | 90.00 | 100.00 | |
Рис. 2.6
6. Отредактировать отчет.
На экране: результат редактирования (рис. 2.7).
Для наглядного представления влияния неиспользуемых финансов на прибыль построим график.
| A | B | C | D | E | F | G | H | I | J | K | L | |
| Прод1 | 11.7 | 13.3 | 12.5 | 7.5 | 2.5 | |||||||
| Прод2 | 0.0 | |||||||||||
| Прод3 | 4.3 | 2.7 | 0.0 | |||||||||
| Прод4 | 0.0 | |||||||||||
| y1 | 3.5 | 8.5 | 13.5 | |||||||||
| y2 | 22.7 | 19.3 | ||||||||||
| Неисп фин | ||||||||||||
| Прибыль |
Рис. 2.7
Алгоритм 2.4. Графическое представление последовательных уступок
1. Выделить A8:L9 (рис. 2.7).
2. Мастер диаграмм:
шаг 2 — График
шаг 3 — Вид2
шаг 4 — 1 стр. метки; 1 столб.
шаг 5 — Убрать легенду, ввести названия графика и осей.
На экране: график последовательных уступок.
3. Выполнить форматирование диаграммы.
На экране: рис. 2.8.

Рис. 2.8
Из таблицы (рис. 2.7) видно, что если мы хотим иметь прибыль, скажем, 1020, то при этом величина неиспользуемых финансов будет равна 30. Если же мы хотим иметь неиспользованных финансов 60, то прибыль при этом будет равна b00.
Таким образом, пользуясь этим алгоритмом и графиком, можно находить соответствующие значения искомых величин, которые могут быть полезны при анализе, выполняемом на этапе принятия оптимального решения.
3. Задачи сравнения вариантов
3.1. Оценка вариантов по обобщенному критерию
Задача сравнения и выбора вариантов возникает очень часто. Для решения этой задачи, прежде всего, каждый вариант необходимо оценить количественно. Такая опенка может быть выполнена с применением всех тех методов, которые были описаны в разделе 1 при рассмотрении коэффициентов веса. Оценка и сравнение вариантов производится с помощью обобщенного критерия, который принимаем в виде
 (3.1)
(3.1)
где  — значение обобщенного критерия для s-ro варианта,
— значение обобщенного критерия для s-ro варианта,
 — коэффициент веса i-ro параметра,
— коэффициент веса i-ro параметра,
 — значение i-ro параметра для s-ro варианта,
— значение i-ro параметра для s-ro варианта,
 — нормирующее значение для i-ro параметра, m — количество параметров.
— нормирующее значение для i-ro параметра, m — количество параметров.
Определение коэффициентов веса производится теми же методами, которые были рассмотрены в разделе 1. В качестве нормирующего значения  принимается либо заданное значение
принимается либо заданное значение  , либо некоторое значение, принимаемое за
, либо некоторое значение, принимаемое за  .
.
Структура обобщенного критерия (3.1) аналогична структуре обобщенной целевой функции (1.1.). однако не следует забывать, что с помощью обобщенного критерия производится оценка и сравнение имеющихся вариантов, в то время как с помощью целевой функции производится определение таких значений параметров, которые обеспечивают максимизацию или минимизацию ее значения. Сравниваемые варианты характеризуются, как правило, тремя основными параметрами:
производительностью;
качеством;
стоимостью.
Оценка и сравнение вариантов производятся по следующим алгоритмам.
Алгоритм 3.1. Оценка вариантов по обобщенному критерию
1. Провести экспертную оценку важности параметров. Результаты экспертизы приведены на рис. 3.1.
| A | B | C | D | E | |
| Эксперт | Производит. | Надежность | Стоимость | ||
| 0,5 | 0,3 | 0,2 | |||
| 0,4 | 0,5 | 0,1 | |||
| 0,6 | 0,2 | 0,2 | |||
| 0,3 | 0,3 | 0,4 | |||
| 0,5 | 0,2 | 0,3 | |||
| a | 0,46 | 0,3 | 0,24 |
Рис. 3.1
2. Составить таблицу для расчета по зависимости (3.1).
Таблица с формулами представлена на рисунке 3.2, таблица с данными – на рис. 3.3.
| A | B | C | D | E | F | G | H | I | |
| Вариант | Произв. | Надежность | Стоимость | Слагаемые | Критерий | ||||
| Альфа | =C$8*C3/C$9 | =D$8*D3/D$9 | =E$8*E3/E$9 | =F3+G3-H3 | |||||
| Бета | =C$8*C4/C$9 | =D$8*D4/D$9 | =E$8*E4/E$9 | =F4+G4-H4 | |||||
| Гамма | =C$8*C5/C$9 | =D$8*D5/D$9 | =E$8*E5/E$9 | =F5+G5-H5 | |||||
| Дельта | =C$8*C6/C$9 | =D$8*D6/D$9 | =E$8*E6/E$9 | =F6+G6-H6 | |||||
| Омега | =C$8*C7/C$9 | =D$8*D7/D$9 | =E$8*E7/E$9 | =F7+G7-H7 | |||||
| коэф.веса | |||||||||
| норма |
Рис.3.2
3. Ввести полученные значения экспертных оценок (рис. 3.1) в ячейки С8:Е8 (рис.3.3).
4. Принять нормирующее значение для параметров и ввести их в ячейки С9:Е9 (рис. 3.3).
| A | B | C | D | E | F | G | H | I | |
| Вариант | Произв. | Надежность | Стоимость | Слагаемые | Критерий | ||||
| Альфа | 0,41 | 0,32 | 0,29 | 0,45 | |||||
| Бета | 0,45 | 0,36 | 0,34 | 0,47 | |||||
| Гамма | 0,48 | 0,31 | 0,36 | 0,43 | |||||
| Дельта | 0,48 | 0,28 | 0,26 | 0,49 | |||||
| Омега | 0,53 | 0,25 | 0,31 | 0,47 | |||||
| коэф.веса | 0,46 | 0,3 | 0,24 | ||||||
| норма | |||||||||
| Вариант | Критерий | № | Вариант | Критерий | |||||
| Альфа | 0,45 | Альфа | 0,45 | ||||||
| Бета | 0,47 | Бета | 0,47 | ||||||
| Гамма | 0,43 | Гамма | 0,43 | ||||||
| Дельта | 0,51 | Дельта | 0,51 | ||||||
| Омега | 0,47 | Омега | 0,47 |
Рис. 3.3
5. Ввести исходные данные: принимаемые значения параметров сравниваемых вариантов в ячейки СЗ:Е7 (рис. 3.3). В рассматриваемом примере качество оценивается надежностью, измеряемой в часах наработки на отказ.
На экране: рис 3.3 (в ячейках I3:I7 значение критерия для каждого варианта).
Алгоритм 3.2. Сравнение вариантов
1. Ячейки В2:В7 (рис.3.3) скопировать в блок С13:С18.
2. Для ячеек 12:17, содержащих значения критерия, выполнить следующее:
Выделить I3:I7.
Копировать в буфер.
Курсор в D13.
Правка, Специальная вставка..., значения.
ОК.
На экране: в D13:D18 скопированы значения критериев.
3. Блок C13:D18 скопировать в Н13:H18.
4. Выполнить сортировку вариантов:
Ø Курсор в любую ячейку блока HI 3:118.
Ø Данные, Сортировка...
Ø Критерий, по убыванию.
Ø ОК.
5. В ячейки 013:018 ввести порядковые номера.
На экране: в ячейках 013:118 приведены сравнительные варианты по мере убывания величины обобщенного критерия.
Следует иметь в виду, что выполненная оценка рассмотренных вариантов не является абсолютной истиной. Это просто оценка по обобщенному критерию для принятых значений:
а коэффициентов веса;
а нормирующих величин параметров.
Очевидно, что при других принимаемых значениях этих величин обобщенный критерий может иметь другие значения.
Таким образом, вариант, выбранный как лучший, является таковым лишь в смысле принятого критерия при заданных нормирующих значениях параметров и назначенных коэффициентах веса. При изменении вида критерия, значений нормирующих элементов или коэффициентов веса лучшим может оказаться совершенно другой вариант. Об этом ни в коем случае нельзя забывать, отдавая предпочтение выбранному варианту.
3.2. Учет разброса экспертных оценок
Коэффициенты веса, которые назначают эксперты, по своей сути являются случайными величинами, поэтому при решении ответственных задач сравнения вариантов следует выполнять действия в соответствии с правилами обработки случайных величин. Такие действия сводятся к следующему.
1. Необходимо определить

где 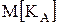 ,
,  D[Kn] — математическое ожидание и дисперсия критерия сравниваемого варианта А, определенные на основании обработки полученных экспертных оценок, n — число экспертов.
D[Kn] — математическое ожидание и дисперсия критерия сравниваемого варианта А, определенные на основании обработки полученных экспертных оценок, n — число экспертов.
2. На основании вычисленного tрасч с помощью функции распределения Стьюдента определить Рдост — достоверность различия сравниваемых вариантов.
Эти работы выполняются по следующему алгоритму.
Алгоритм 3.3. Определение математических ожиданий и дисперсий критериев
1. Для экспертных оценок (рис. 3.1) определить их математические ожидания и дисперсии. Необходимая для этого таблица с формулами приведена на рис. 3.4, таблица с данными — на рис. 3.5.
| A | B | C | D | E | |
| Эксперт | Производит. | Надежность | Стоимость | ||
| M[a] | =СРЗНАЧ(C3:C7) | =СРЗНАЧ(D3:D7) | =СРЗНАЧ(E3:E7) | ||
| D[a] | =ДИСП(C3:C7) | =ДИСП(D3:D7) | =ДИСП(E3:E7) | ||
| V[a] | =КОРЕНЬ(C9)/C8 | =КОРЕНЬ(D9)/D8 | =КОРЕНЬ(E9)/E8 |
Рис. 3.4
| A | B | C | D | E | |
| Эксперт | Производит. | Надежность | Стоимость | ||
| 0,5 | 0,3 | 0,2 | |||
| 0,4 | 0,5 | 0,1 | |||
| 0,6 | 0,2 | 0,2 | |||
| 0,3 | 0,3 | 0,4 | |||
| 0,5 | 0,2 | 0,3 | |||
| M[a] | 0,46 | 0,3 | 0,24 | ||
| D[a] | 0,01 | 0,02 | 0,01 | ||
| V[a] | 0,25 | 0,41 | 0,48 |
Рис. 3.5
2. Сформировать таблицу для определения математического ожидания и дисперсии критериев сравниваемых вариантов. Таблица с формулами показана на рис. 3.6, таблица с данными — на рис. 3.7.
| A | B | C | D | E | F | G | H | |
| Вариант | Произв | Надеж | Стоим | |||||
| Альфа | =C$8*C3/C$10 | =D$8*D3/D$10 | =E$8*E3/E$10 | |||||
| Бета | =C$8*C4/C$10 | =D$8*D4/D$10 | =E$8*E4/E$10 | |||||
| Гамма | =C$8*C5/C$10 | =D$8*D5/D$10 | =E$8*E5/E$10 | |||||
| Дельта | =C$8*C6/C$10 | =D$8*D6/D$10 | =E$8*E6/E$10 | |||||
| Омега | =C$8*C7/C$10 | =D$8*D7/D$10 | =E$8*E7/E$10 | |||||
| M[] | ||||||||
| D[] | ||||||||
| норма |
| I | J | K | L | M | |
| M[Kр] | D[Kр] | ||||
| =F3+G3-H3 | =C$9*C3/C$10 | =D$9*D3/D$10 | =E$9*E3/E$10 | =J3+K3+L3 | |
| =F4+G4-H4 | =C$9*C4/C$10 | =D$9*D4/D$10 | =E$9*E4/E$10 | =J4+K4+L4 | |
| =F5+G5-H5 | =C$9*C5/C$10 | =D$9*D5/D$10 | =E$9*E5/E$10 | =J5+K5+L5 | |
| =F6+G6-H6 | =C$9*C6/C$10 | =D$9*D6/D$10 | =E$9*E6/E$10 | =J6+K6+L6 | |
| =F7+G7-H7 | =C$9*C7/C$10 | =D$9*D7/D$10 | =E$9*E7/E$10 | =J7+K7+L7 | |
Рис. 3.6
| A | B | C | D | E | F | G | H | I | J | K | L | M | |
| Вариант | Произв | Надеж | Стоим | M[K] | D[K] | ||||||||
| Альфа | 0,41 | 0,32 | 0,29 | 0,45 | 0,009 | 0,021 | 0,012 | 0,042 | |||||
| Бета | 0,45 | 0,36 | 0,34 | 0,47 | 0,010 | 0,024 | 0,014 | 0,048 | |||||
| Гамма | 0,48 | 0,31 | 0,36 | 0,43 | 0,010 | 0,021 | 0,015 | 0,046 | |||||
| Дельта | 0,50 | 0,28 | 0,26 | 0,51 | 0,011 | 0,019 | 0,011 | 0,040 | |||||
| Омега | 0,53 | 0,25 | 0,31 | 0,47 | 0,012 | 0,017 | 0,013 | 0,015 | |||||
| M[] | 0,46 | 0,3 | 0,24 | ||||||||||
| D[] | 0,01 | 0,02 | 0,01 | ||||||||||
| норма |
Рис. 3.7
В этих таблицах для определения искомых величин используются следующие зависимости:


где  ,
,  — величина i-гo параметра для варианта А и нормирующее значение для всех вариантов данного параметра.
— величина i-гo параметра для варианта А и нормирующее значение для всех вариантов данного параметра.
3. Ввести в таблицу (рис. 3.7) исходные данные (рис. 3.3):
значения производительности, надежности и стоимости для всех вариантов, а также нормирующие значения для вводимых величин.
4. Ввести в таблицу (рис. 3.7) математические ожидания и дисперсии коэффициентов веса (рис. 3.5).
На экране: рис. 3.7, на котором для всех вариантов значения математических ожиданий М[К] находятся в ячейках I4:I8, а значения дисперсий D[K.n] — в ячейках М4:М8. Эти величины выделены тенью и жирным шрифтом.
5. Полученные значения математического ожидания и дисперсии критериев скопировать в ячейки B3:D8 (рис. 3.8).
| A | B | C | D | A | B | C | D | ||||
| Вариант | М[K] | D[K] | Вариант | М[K] | D[K] | ||||||
| Альфа | 0,45 | 0,042 | Дельта | 0,51 | 0,042 | ||||||
| Бета | 0,47 | 0,048 | Бета | 0,47 | 0,049 | ||||||
| Гамма | 0,43 | 0,046 | Омега | 0,47 | 0,044 | ||||||
| Дельта | 0,51 | 0,040 | Альфа | 0,45 | 0,043 | ||||||
| Омега | 0,47 | 0,015 | Гамма | 0,43 | 0,049 |
Рис. 3.8 Рис. 3.9
6. Выполнить сортировку этих значений по убыванию М[К], как это описано в алг. 3.2.
На экране: результат сортировки (рис. 3.9) в ячейках B2:D7.
После этого следует приступить к определению достоверности различия критериев для каждой пары сравниваемых вариантов.
Алгоритм 3.4. Определение достоверности различия вариантов
1. Сформировать таблицу для определения tрзсч по зависимости (3.2) для каждой пары сравниваемых вариантов. Такая таблица с формулами приведена на рис. 3.10.
| G | H | I | J | |
| Вариант | Дельта | Бета | Омега | |
| Дельта | X | =ABS($C$4-$C$5)/КОРЕНЬ(($D$4+$D$5)/5) | =ABS($C$4-$C$6)/КОРЕНЬ(($D$4+$D$6)/5) | |
| Бета | =I4 | X | =ABS($C$5-$C$6)/КОРЕНЬ(($D$5+$D$6)/5) | |
| Омега | =J4 | =J5 | X | |
| Альфа | =K4 | =K5 | =K6 | |
| Гамма | =L5 | =L6 | =L6 |
| K | L | |
| Альфа | Гамма | |
| =ABS($C$4-$C$7)/КОРЕНЬ(($D$4+$D$7)/5) | =ABS($C$4-$C$8)/КОРЕНЬ(($D$4+$D$8)/5) | |
| =ABS($C$5-$C$7)/КОРЕНЬ(($D$5+$D$7)/5) | =ABS($C$5-$C$8)/КОРЕНЬ(($D$5+$D$8)/5) | |
| =ABS($C$6-$C$7)/КОРЕНЬ(($D$6+$D$7)/5) | =ABS($C$6-$C$8)/КОРЕНЬ(($D$6+$D$8)/5) | |
| X | =ABS($C$7-$C$8)/КОРЕНЬ(($D$7+$D$8)/5) | |
| =L7 | X |
Рис. 3.10
Таблица со значениями tрасч после ввода значений М[К] и D[K] из рис. 3.9 приведена на рис. 3.11.
| G | H | I | J | K | L | |
| tрасч | ||||||
| Вариант | Дельта | Бета | Омега | Альфа | Гамма | |
| Дельта | X | 0,261 | 0,291 | 0,489 | 0,605 | |
| Бета | 0,261 | Х | 0,023 | 0,212 | 0,332 | |
| Омега | 0,291 | 0,023 | Х | 0,193 | 0,317 | |
| Альфа | 0,489 | 0,212 | 0,193 | Х | 0,13 | |
| Гамма | 0,605 | 0,332 | 0,317 | 0,13 | Х |
Рис. 3.11
2. Определить достоверность различия сравниваемых вариантов. Искомая достоверность определяется с помощью функции Excel, которая вызывается командами Мастер функций, Статистические, СТЬЮДРАСП и имеет формат
СТЬЮДРАСП(tрасч; f, а).
где tрасч — величины, определенные в таблице на рис. 3.11,
f — число степеней свободы: f = 2(п - 1), где n — число экспертов, в рассматриваемом примере f= 2*(5 -1) = 8,
а — тип распределения Стьюдента, в нашем случае а = 2.
При работе с этой функцией следует иметь в виду, что функция Excel СТЬЮДРАСП () определяет вероятность того, что сравниваемые варианты не различаются, поэтому для решения задачи определения достоверности различия следует вычислять величину
Рразл= 1 -СТЬЮДРАСП().
Формулы для вычисления этой величины введены в ячейки таблицы, показанной на рис. 3.12. Количественные значения достоверности различия вариантов для данных (рис 3.9) приведены в таблице на рис. 3.13, из которой видно, что достоверность различия сравниваемых вариантов невелика.
| G | H | I | J | K | L | |
| Достоверность различия | ||||||
| Вариант | Дельта | Бета | Омега | Альфа | Гамма | |
| Дельта | X | =1-СТЬЮДРАСП(I4;8;2) | =1-СТЬЮДРАСП(J4;8;2) | =1-СТЬЮДРАСП(K4;8;2) | =1-СТЬЮДРАСП(L4;8;2) | |
| Бета | =I14 | X | =1-СТЬЮДРАСП(J5;8;2) | =1-СТЬЮДРАСП(K5;8;2) | =1-СТЬЮДРАСП(L5;8;2) | |
| Омега | =I15 | =J15 | X | =1-СТЬЮДРАСП(K6;8;2) | =1-СТЬЮДРАСП(L6;8;2) | |
| Альфа | =I16 | =K15 | =K16 | X | =1-СТЬЮДРАСП(L7;8;2) | |
| Гамма | =I17 | =L15 | =L16 | =L17 | X |
Рис. 3.12
| G | H | I | J | K | L | |
| Вариант | A | B | C | D | E | |
| A | X | 0,20 | 0,22 | 0,36 | 0,44 | |
| B | 0,20 | X | 0,02 | 0,16 | 0,25 | |
| C | 0,22 | 0,02 | X | 0,15 | 0,24 | |
| D | 0,36 | 0,16 | 0,15 | X | 0,10 | |
| E | 0,44 | 0,25 | 0,24 | 0,10 | X |
Рис. 3.13
Для получения более значительных различий между сравниваемыми вариантами выполним алг. 3.4 с исходными данными для других вариантов. Эти исходные данные, в которых значения М[К] в отличие от данных, рассмотренных выше, различаются более существенно, приведены на рис. 3.14.
| A | B | C | D | |
| Вариант | M[K] | D[K] | ||
| A | 1,00 | 0,010 | ||
| B | 0,90 | 0,010 | ||
| C | 0,70 | 0,044 | ||
| D | 0,60 | 0,043 | ||
| E | 0,40 | 0,049 |
Рис. 3.14
Формулы для вычисления значения tрaсч для новых вариантов представлены на рис. 3.15, вычисленные значения — на рис. 3.16.
| G | H | I | J | |
| t расч | ||||
| Вариант | A | B | C | |
| A | X | =ABS($C$4-$C$5)/КОРЕНЬ(($D$4+$D$5)/5) | =ABS($C$4-$C$6)/КОРЕНЬ(($D$4+$D$6)/5) | |
| B | =I4 | X | =ABS($C$5-$C$6)/КОРЕНЬ(($D$5+$D$6)/5) | |
| C | =J4 | =J5 | X | |
| D | =K4 | =K5 | =K6 | |
| E | =L5 | =L6 | =L6 |
| K | L | |
| D | E | |
| =ABS($C$4-$C$7)/КОРЕНЬ(($D$4+$D$7)/5) | =ABS($C$4-$C$8)/КОРЕНЬ(($D$4+$D$8)/5) | |
| =ABS($C$5-$C$7)/КОРЕНЬ(($D$5+$D$7)/5) | =ABS($C$5-$C$8)/КОРЕНЬ(($D$5+$D$8)/5) | |
| =ABS($C$6-$C$7)/КОРЕНЬ(($D$6+$D$7)/5) | =ABS($C$6-$C$8)/КОРЕНЬ(($D$6+$D$8)/5) | |
| X | =ABS($C$7-$C$8)/КОРЕНЬ(($D$7+$D$8)/5) | |
| =L7 | X |
Рис. 3.15
| G | H | I | J | K | L | |
| t расч | ||||||
| Вариант | A | B | C | D | E | |
| A | X | 1,581 | 2,874 | 3,874 | 5,546 | |
| B | 1,581 | X | 1,916 | 2,906 | 4,622 | |
| C | 2,874 | 1,916 | X | 0,755 | 2,200 | |
| D | 3,874 | 2,906 | 0,755 | X | 1,476 | |
| E | 4,622 | 2,200 | 2,200 | 1,476 | X |
Рис. 3.16
Формулы для вычисления достоверности различия новых сравниваемых вариантов приведены на рис. 3.17, а вычисленные значения достоверности для них — на рис. 3.18. Из таблицы на рис. 3.18 видно, что достоверность различия сравниваемых вариантов в данном случае достаточно высока.
| G | H | I | J | K | L | |
| Достоверноверность различия | ||||||
| Вариант | A | B | C | D | E | |
| A | X | =1-СТЬЮДРАСП(I4;8;2) | =1-СТЬЮДРАСП(I4;8;2) | =1-СТЬЮДРАСП(I4;8;2) | =1-СТЬЮДРАСП(I4;8;2) | |
| B | =I14 | X | =1-СТЬЮДРАСП(I5;8;2) | =1-СТЬЮДРАСП(I5;8;2) | =1-СТЬЮДРАСП(I5;8;2) | |
| C | =J14 | =J15 | X | =1-СТЬЮДРАСП(I6;8;2) | =1-СТЬЮДРАСП(I6;8;2) | |
| D | =K14 | =K15 | =K16 | X | =1-СТЬЮДРАСП(I7;8;2) | |
| E | =L14 | =L15 | =L16 | =L17 | X |
Рис. 3.17
| G | H | I | J | K | L | |
| Достоверноверность различия | ||||||
| Вариант | A | B | C | D | E | |
| A | X | 0,85 | 0,980 | 1,00 | 1,00 | |
| B | 0,85 | X | 0,910 | 0,98 | 1,00 | |
| C | 0,98 | 0,91 | X | 0,53 | 0,94 | |
| D | 1,00 | 0,98 | 0,53 | X | 0,82 | |
| E | 1,00 | 1,00 | 0,94 | 0,82 | X |
Рис. 3.18
Приведенные примеры убедительно показывают, что при сравнении и выборе вариантов неучет достоверности их различия может привести к принятию не достаточно обоснованных решений.
Поиск по сайту: