Ключ к контрольно-измерительным материалам

III семестр

Часть 1

№ вопроса	Вариант
	б	а	в	а	в	б	а	г, б, в, а	б	в, г
	г	а	б	б	в	а	б	г	г	а
	в	в	б	в	в	а	г	б	в	б
	б	г	а	а	б	б	б	1-в 2-б 3-а	в	в
	а	в	г	б	б	в	а	г	г	б
	б	б	а	а	а	б	б	б	а, в	в
	б	б	в	в	б	а	а, б	а	г, б, в, а	б
	в	в	в	в	а	а	в	а	в	в
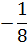
		г	г	б	в		а	в	б
		а	а		а	-7	б	а	б

Часть 2

Вариант	№ вопроса
	(-2; 2; 1; -1)	-1.5
	52°	34.5
	8; 0.8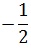
	нет
		34.5
	6x-5y-30=0	52°
	нет
	34,5	(-2; 2; 1; -1)
	(-2; 2; 1; -1)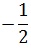
		6x-5y-30=0

Часть 3

Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5
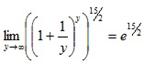
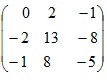
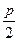
Вариант 6	Вариант 7	Вариант 8	Вариант 9	Вариант 10
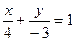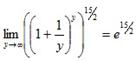
6 кв. ед.			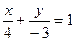6 кв. ед.	X1=-1 X2=-3 X3=0 X4=0

Решения части 3

Вариант 1.

Решение:

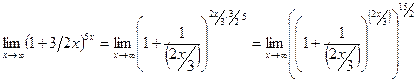
Заменяя 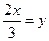и учитывая, что y → ∞ при x → ∞, можем написать

.

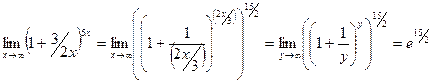Вариант 2

Решение:

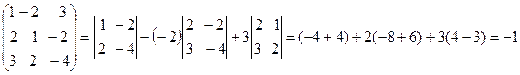
Составим союзную матрицу. Для этого вычислим алгебраические дополнения:

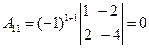
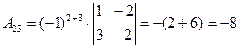
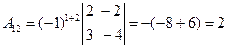
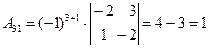
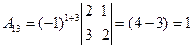
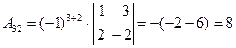
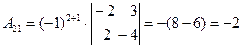
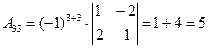
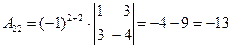
Союзная матрица будет следующей: 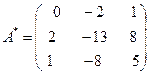. Вычислим обратную матрицу:

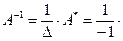
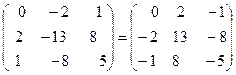
Проверкой 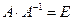убеждаемся, что обратная матрица найдена верно.

Вариант 3

Решение:

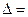
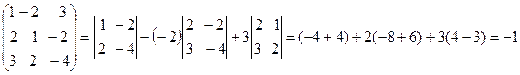
Составим союзную матрицу. Для этого вычислим алгебраические дополнения:

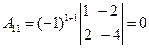
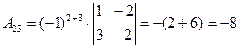
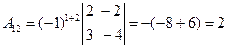
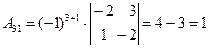
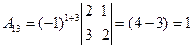
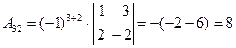
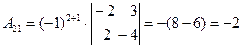
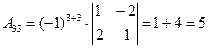
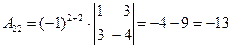
Союзная матрица будет следующей: 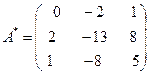. Вычислим обратную матрицу:

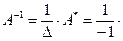
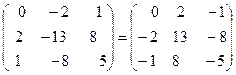
Найдем решение системы по формуле

.

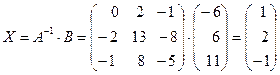Вариант 4

Решение:

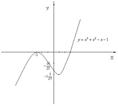
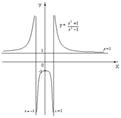
исследуем функцию по схеме:

1. D(y)=R;

2. 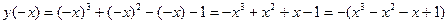- функция не будет ни четной, ни нечетной; функция непериодическая;

3. Найдем точки пересечения с (ОХ): 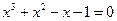. Перебирая делители свободного члена, находим целые нули функции: .

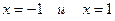Найдем точки пересечения графика функции с осью (ОУ): если 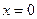, то ;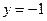

4. Асимптот нет;

5. Для нахождения интервалов монотонности функции найдем ее производную: 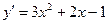. Найдем критические точки функции: 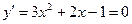. Получим: 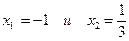. Найдем интервалы возрастания и убывания функции:

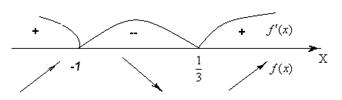
Из чертежа имеем, что функция возрастает на 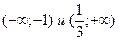, убывает на 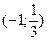. Найдем экстремумы функции:

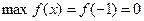. Значит, точка максимума имеет координаты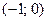

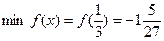. Значит, точка минимума имеет координаты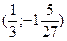

6. Для нахождения интервалов выпуклости графика функции вычислим вторую

производную: 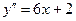. Найдем критические точки 2 рода функции:

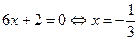. Определим знак второй производной в интервалах, на которые разбивается область определения

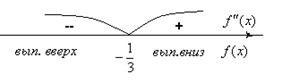
Значит, график функции будет выпуклым вверх на 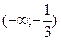и выпуклым вниз на 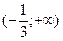. Т.к. вторая производная меняет знак при переходе через точку 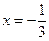, то в ней график будет иметь перегиб. Вычислим: 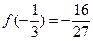. Значит, точка перегиба .

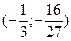7. Построим график:

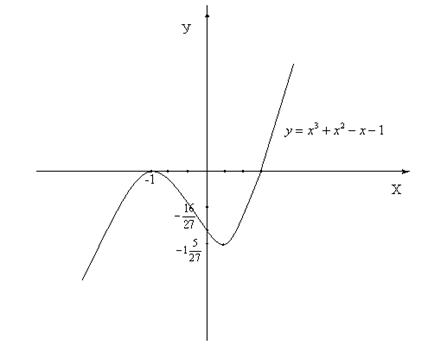
Вариант 5

Решение:

Из условий задачи имеем, что периметр участка равен 2р. Обозначим длины сторон прямоугольника х и у. Тогда из периметра прямоугольника имеем

.

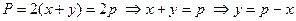Обозначим через S(x) площадь прямоугольника. Тогда 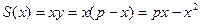, причем 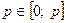. Исследуем полученную функцию на экстремум: 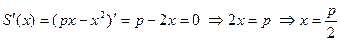- критическая точка, принадлежащая отрезку 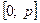. Исследуя знак 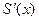в интервалах 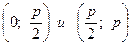, получаем, что на первом из них S(x) возрастает, а на втором убывает. Следовательно, при 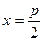площадь прямоугольника будет наибольшей. Найдем 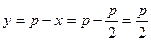. Значит, из прямоугольников с периметром 2р, наибольшую площадь будет иметь квадрат со стороной .

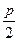Вариант 6.

Решение:

Преобразуем данное уравнение следующим образом: 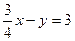, или .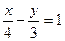

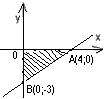
В результате получим уравнение 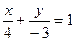, которое и является уравнением данной прямой в отрезках. Треугольник, образованный данной прямой и осями координат, является прямоугольным треугольником с катетами, равными 4 и 3, поэтому его площадь равна S= 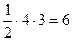(кв. ед.)

Вариант 7.

Решение:

Заменяя 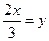и учитывая, что y → ∞ при x → ∞, можем написать

.

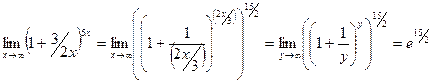Вариант 8

Решение:

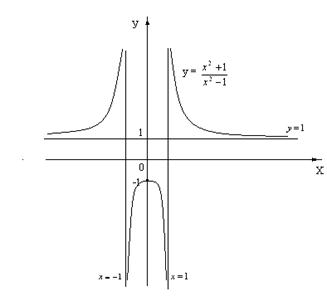
1. Найдем область определения функции. Она задается условиями x ≠ 1, x ≠ -1 (при значениях x ≠ 1, x ≠ -1 знаменатель дроби обращается в нуль). Итак, D(f)=(-∞;1)(-1:1)(1;+∞).

2. Исследуем функцию на честность:

f 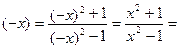f (x)

Значит, заданная функция четна, ее график симметричен относительно оси ординат, а потому можно для начала ограничиться построением ветвей графика при x ≥ 0.

3. Точек пересечения графика функции с осью ОХ нет,

Найдем точки пересечения графика функции с осью ОУ: если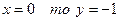

4. Найдем асимптоты графика. Вертикальной асимптотой является прямаяx = 1, поскольку при этом значении x знаменатель дроби обращается в нуль, а числитель отличен от нуля. Для отыскания горизонтальной асимптоты надо вычислить 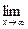f (x):

^.

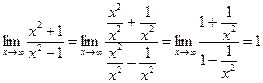Значит, y = 1 – горизонтальная асимптота графика функции.

5. Найдем критические точки, точки экстремума и промежутки монотонности функции:

y′ .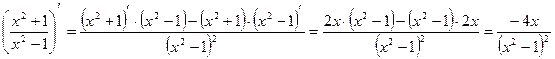

Критические точки найдем из соотношения y^´ = 0. Получаем –4x = 0, откуда находим, что х = 0. При х < 0 имеем y^´> 0, а при х > 0 имеем y^´< 0. Значит, х = 0 – точка максимума функции, причем у_max= f (0)= .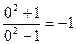

При х > 0 имеем y^´< 0, но следует учесть наличие точки разрыва х = 1. Значит, вывод о промежутках монотонности будет выглядеть так: на промежутке [0;1) функция убывает, на промежутке (1;+∞) функция также убывает.

1.

2.

3.

4.

5.

6. Вычислим вторую производную:

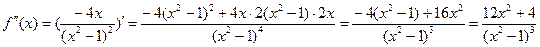
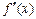нигде не обращается в ноль, критическими точками будут только точки .

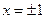Определим знак 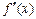в интервалах:

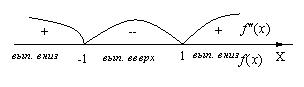
7. Отметим (0;-1) – точку максимума, построим прямые у = 1 – горизонтальную асимптоту, что x = 1 и x = - 1– вертикальные асимптоты;

Вариант 9

Решение:

Преобразуем данное уравнение следующим образом: 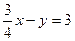, или .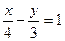

В результате получим уравнение 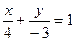, которое и является уравнением данной прямой в отрезках. Треугольник, образованный данной прямой и осями координат, является прямоугольным треугольником с катетами, равными 4 и 3, поэтому его площадь равна S= 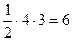(кв. ед.)

Вариант 10

Решение.

В результате элементарных преобразований над расширенной матрицей системы:

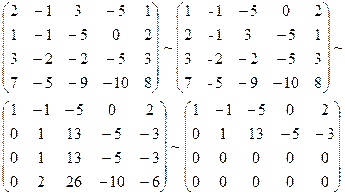
Исходная система свелась к ступенчатой:

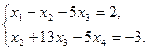
Поэтому общее решение системы: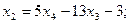

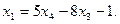
Если положить, например, 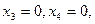найдем одно из частных решений этой системы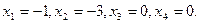

Поиск по сайту: