 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
IV СЕМЕСТР
Часть 1
| Вариант | Номер вопроса | |||||||||
| в | в | а | в | б | а | а | б | а | а | |
| б | в | в | в | б | б | а | г | в | б | |
| а | б | а | в | б | г | б | в | в | а | |
| б | б | а | б | б | а | а | г | в | ||
| б | в | в | б | в | б | б | в | в | ||
| в | -16 | а | в | б | б | а | г | б | а | |
| в | б | а | в | а | а | б | а | а | г | |
| в | в | а | а | б | а | а | г | а | в | |
| а | а | а | а | б | а | а | в | в | б | |
| б | в | в | в | в | г | в | а | б | в |
Часть 2
| Вариант | № вопроса | |
| R = 3 | 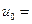 1; 1; 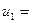 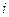 ; ; 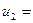 -1; -1; 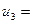 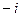
| |
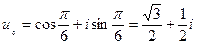
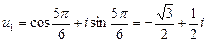
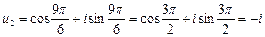
| Область определения есть I-ая четверть плоскости хОу | |
у: 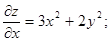 х:
х: 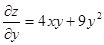
| 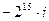
| |
| ||
| ||
| 
| |
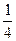
| 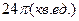
| |
| -1 | 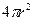
| |
df(xy)=7dx+3 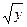 dx+12ydy- dx+12ydy- 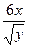 dy dy
| 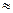 2,4(ед) 2,4(ед)
| |
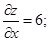 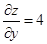
| 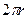
|
Часть 3
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 |
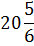
|
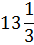
|
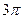
|
| |
| Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 |
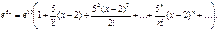
|
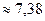
|
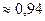
|
|
Ответы на часть 3:
Используемые формулы в решении задач 3 части:
1) 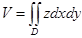 (1)
(1)
2) 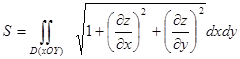 (2)
(2)
3) 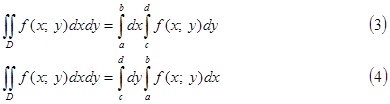
4) 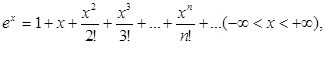 (5)
(5)
5) 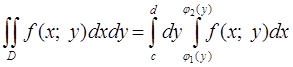 (6)
(6)
Вариант 1
Решение: Найдем точки пересечения данных линий, для этого решим систему уравнений:
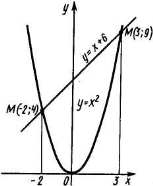
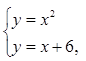
Решением будет пара значений (-3; 9) и (-2; 4) - координаты точек пересечения графиков
Область D запишем в виде системы неравенств
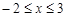 ,
, 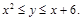
Согласно формуле (1), получим
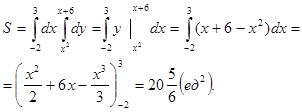
Вариант 2
Решение: Тело, ограниченное заданными поверхностями, представляет собой вертикальный параболический цилиндр, расположенный в I октанте. Сверху тело ограничено плоскостью z = 2x+1, сбоку параболическим цилиндром у =x 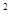 и плоскостями х = 0 и у = 4, снизу
и плоскостями х = 0 и у = 4, снизу
параболой у =x 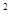 и прямыми х = 0 и у = 4. Найдем точки пересечения параболы у =x
и прямыми х = 0 и у = 4. Найдем точки пересечения параболы у =x 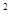 и прямой у = 4:
и прямой у = 4:
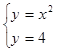
Получаем два решения: (-2; 4) и (2; 4). Значение 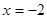 не рассматриваем, т.к. цилиндр расположен в I октанте. Область D запишем в виде системы неравенств 0 ≤ x ≤ 2, x
не рассматриваем, т.к. цилиндр расположен в I октанте. Область D запишем в виде системы неравенств 0 ≤ x ≤ 2, x 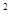 ≤ y ≤ 4. Согласно формуле (3), получим
≤ y ≤ 4. Согласно формуле (3), получим
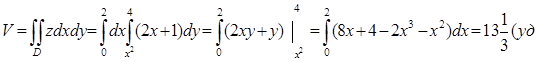
Вариант 3
Решение: Данное тело есть прямой круговой цилиндр, ограниченный сверху плоскостью
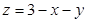 , а снизу — кругом
, а снизу — кругом 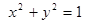 в плоскости z=0. Область D в основании цилиндра запишем в виде системы неравенств
в плоскости z=0. Область D в основании цилиндра запишем в виде системы неравенств
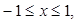
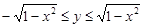
Согласно формуле (1), получим
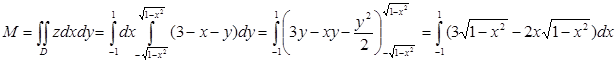
Первый интеграл табличный и равен:
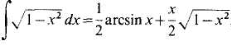
Второй интеграл вычисляется подстановкой 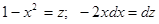 ;следовательно, второй интеграл равен:
;следовательно, второй интеграл равен:
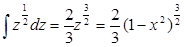
Окончательно находим
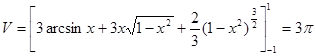 (куб. ед.).
(куб. ед.).
Вариант 4
Решение: найдем отрезки, отсекаемые на координатных осях данной плоскостью:
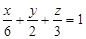 ,
, 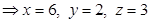
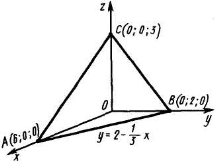
Чтобы воспользоваться формулой (2), решим уравнение данной плоскости относительно переменной z и найдем частные производные:
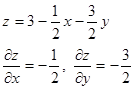
При z = 0 имеем х + 3у = 6, откуда 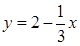 ; следовательно, в плоскости z = 0 область D запишется в виде системы неравенств
; следовательно, в плоскости z = 0 область D запишется в виде системы неравенств
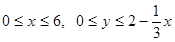 . Тогда
. Тогда
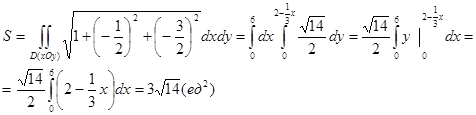
Вариант 5
Решение: искомая поверхность образована пересечением двух цилиндров 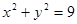 и
и 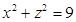 . В эти уравнения поверхностей входят квадраты переменных, поэтому искомая поверхность симметрична относительно каждой из координатных плоскостей и для вычисления рассмотрим 1/8 ее часть, лежащую в I октанте.
. В эти уравнения поверхностей входят квадраты переменных, поэтому искомая поверхность симметрична относительно каждой из координатных плоскостей и для вычисления рассмотрим 1/8 ее часть, лежащую в I октанте.
Область интегрирования D представляет собой 1/4 часть круга 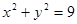 , заключенного между положительными полуосями Ох и Оу, и определяется системой неравенств
, заключенного между положительными полуосями Ох и Оу, и определяется системой неравенств 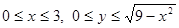
Из уравнения 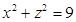 имеем
имеем 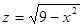 . Далее, находим частные производные
. Далее, находим частные производные
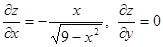 , откуда
, откуда 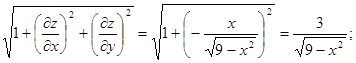
Следовательно, 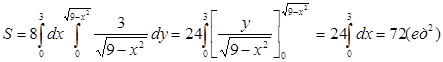
Вариант 6
Решение: вычислим значения данной функции и ее последовательных производных при х = 2:
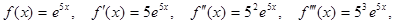 …,
…, 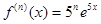
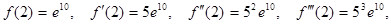 …,
…, 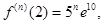
Подставляя найденные значения и общее выражение ряда Тейлора для производной функции, получим 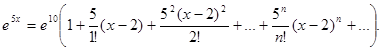 Это и есть разложение ряд Тейлора по степеням (х – 2) для функции
Это и есть разложение ряд Тейлора по степеням (х – 2) для функции 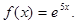 Полученный ряд сходится к порождающей его функции
Полученный ряд сходится к порождающей его функции 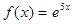 при любом значении х. Заметим, что искомое разложение можно получить также следующим образом. В разложение (3) заменим х на 5х; тем самым получим ряд Маклорена для функции
при любом значении х. Заметим, что искомое разложение можно получить также следующим образом. В разложение (3) заменим х на 5х; тем самым получим ряд Маклорена для функции 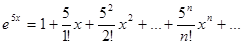 . (*)
. (*)
Представив теперь функцию 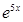 в виде
в виде 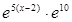 и подставляя в соотношение (*) (х – 2) вместо х, приходим к разложению
и подставляя в соотношение (*) (х – 2) вместо х, приходим к разложению
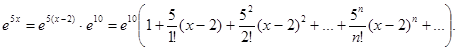
Вариант 7
Решение: пользуясь разложением (5), при х=2 получим
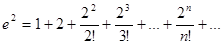 .
.
Остается решить вопрос о том, сколько членов данного ряда надо взять, чтобы получить значение 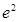 с требуемой точностью. Пусть искомое число членов равно
с требуемой точностью. Пусть искомое число членов равно 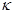 . Это означает, что ошибка
. Это означает, что ошибка 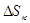 , которую мы допускаем, заменяя сумму ряда его
, которую мы допускаем, заменяя сумму ряда его 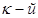 частичной суммой, равна сумме членов ряда, начиная с
частичной суммой, равна сумме членов ряда, начиная с 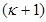 -го:
-го:
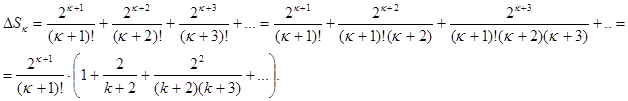
Если заменить каждое из чисел 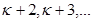 числом
числом 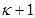 , то знаменатели дробей уменьшается, а сами дроби, следовательно, увеличиваются. Поэтому
, то знаменатели дробей уменьшается, а сами дроби, следовательно, увеличиваются. Поэтому
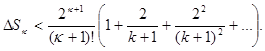 Выражение, стоящие в квадратной скобке, есть сумма членов бесконечно убывающей геометрической прогрессии со знаменателем
Выражение, стоящие в квадратной скобке, есть сумма членов бесконечно убывающей геометрической прогрессии со знаменателем 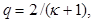 и
и
следовательно, равно 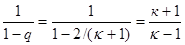 . Таким образом,
. Таким образом,
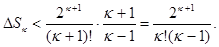
Но, с другой стороны, ошибка 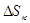 не должна превосходить 0,01:
не должна превосходить 0,01: 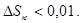 Решая методом подбора неравенство
Решая методом подбора неравенство 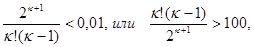
получим 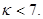 Итак, для достижения требуемой точности надо взять 8 членов ряда:
Итак, для достижения требуемой точности надо взять 8 членов ряда:
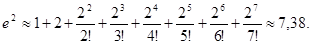
Вариант 8
Решение: данный определенный интеграл можно вычислить только приближенно. Для этого разложим подынтегральную функцию в ряд Тейлора 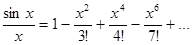 . Отсюда
. Отсюда
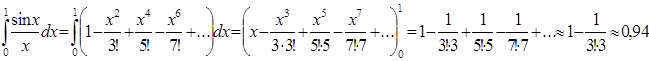
здесь мы ограничились двумя первыми этого знакопеременного ряда, так как третий
член 1/(5!5) меньше 0,01.
Вариант 9
Решение: Область D является простой относительно осей Ох и Оу, поэтому для вычисления интеграла можно использовать любую из формул (3) или (4).
Сначала вычислим двойной интеграл по формуле (3):
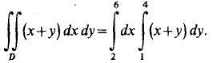
Вычислив внутренний интеграл по переменной у при постоянном х, находим
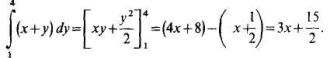
Подставив это выражение во внешний интеграл, получим
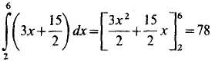
Теперь вычислим двойной интеграл по формуле (4):
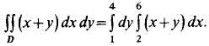
Найдем внутренний интеграл:
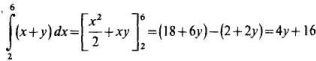
Далее найдем внешний интеграл:
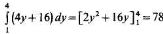
т. е. получили тот же ответ.
Вариант 10
Решение: Согласно формуле (6), имеем
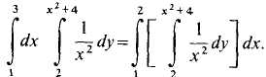
Вычислим сначала внутренний интеграл по переменной у, считая х постоянным:
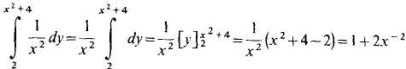
Теперь вычислим внешний интеграл по переменной х, подставив в него полученное выражение:
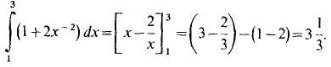
Поиск по сайту: