 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Лекция 5. Надежность элементов колесной пары
Наиболее нагруженным элементом колесной пары является шейка оси. Как показывает опыт эксплуатации, среди всех колесных пар наиболее нагруженной является первая по ходу движения вагона. Связано это с тем, что при вписывании подвижного состава в кривой участок пути кроме вертикальной, статической и динамической нагрузок на шейку передается направляющая сила рельса. При этом соответствующая реакция на поверхности катания колеса приложена в месте контакта с рельсом.
В ряде случаев нагрузки прикладываются к средней части оси, например в месте расположения шкива привода подвагонного генератора или диска тормоза.
Вертикальная статическая нагрузка груженного вагона подсчитывается по формуле
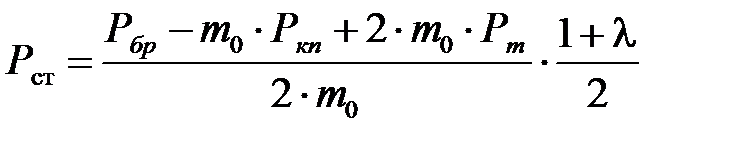 , (5.1)
, (5.1)
где  ,
,  ,
,  – силы тяжести соответствующего вагона брутто, сила тяжести колесной пары и сила тяжести консольной части оси, считая от торца шейки до плоскости круга катания колеса;
– силы тяжести соответствующего вагона брутто, сила тяжести колесной пары и сила тяжести консольной части оси, считая от торца шейки до плоскости круга катания колеса;
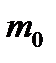 – число колесных пар в вагоне;
– число колесных пар в вагоне;
λ – средняя величина коэффициента использования грузоподъемности вагона, для пассажирского вагона λ = 1.
Вертикальная динамическая нагрузка, возникающая при колебаниях обрессоренных масс, вычисляется по формуле
 , (5.2)
, (5.2)
где  – коэффициент вертикальной динамики колесной пары, определяемый по формуле
– коэффициент вертикальной динамики колесной пары, определяемый по формуле
 (5.3)
(5.3)
где λв – величина, зависящая от осности тележки (приведена в таблице).
А, В – величины, зависящие от типа вагона и жесткости рессорного подвешивания.
 – статический прогиб рессорного подвешивания.
– статический прогиб рессорного подвешивания.
Таблица значений, необходимых при расчете коэффициентов динамики колесных пар
| Тип вагона | Диапазон скорости, м/с | А | В×104 | Д | λв | λг | δ×10-3 |
| грузовой 4-осн | 15–33 | 0,03 | 6,0 | ||||
| грузовой 6-осн | 15–33 | 0,03 | 6,0 | 0,9 | 0,9 | ||
| грузовой 8-осн | 15–33 | 0,03 | 6,0 | 0,8 | 0,8 | 0,8 | |
| изотермический | 33–39 | 0,05 | 5,5 | 0,8 | |||
| пассажирский | 33–39 | 0,06 | 4,5 | 0,8 | |||
| пассажирский | 39–55 | 0,06 | 4,5 | 0,8 |
Схема загруженности колесной пары вагона
 вертикальные статические и динамические силы
вертикальные статические и динамические силы
|  вертикальные силы от горизонтальных нагрузок
вертикальные силы от горизонтальных нагрузок
|
 горизонтальные нагрузки от центробежной силы и ветровой нагрузки
горизонтальные нагрузки от центробежной силы и ветровой нагрузки
|  вертикальные нагрузки от сил инерции необрессоренных масс
вертикальные нагрузки от сил инерции необрессоренных масс
|
При проведении расчета учитывается наиболее неблагоприятное состояние несимметричного вида колебаний. Динамическую нагрузку считают приложенной к центру одной шейки, а на другой ее принимают равной нулю.
Вертикальные реакции от действия статических и динамических сил определяют из условия равновесия колесной пары.
 , (5.4)
, (5.4)
от куда следует выражение
 , (5.5)
, (5.5)
Из условия равновесия колесной пары в вертикальном направлении получаем
 , (5.6)
, (5.6)
откуда получаем
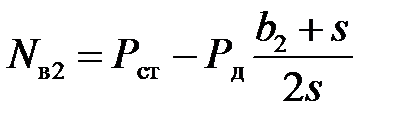 . (5.7)
. (5.7)
Вертикальная нагрузка от центробежной силы, догружает одну шейку и разгружает другую (схема б) эта нагрузка определяется формулой
 , (5.8)
, (5.8)
где  – центробежная сила вагона, отнесенная к одной колесной паре;
– центробежная сила вагона, отнесенная к одной колесной паре;
 – высота центра тяжести вагона над уровнем осевых линий колесных пар;
– высота центра тяжести вагона над уровнем осевых линий колесных пар;
 – расстояние между центрами шеек оси.
– расстояние между центрами шеек оси.
Вертикальная нагрузка от давления ветра (схема б) определяется из условия равновесия вагона с учетом моментов, действующих на вагон
 , (5.9)
, (5.9)
где  – сила давления ветра, действующая на боковую поверхность вагона.
– сила давления ветра, действующая на боковую поверхность вагона.
 – расстояние от равнодействующей давления ветра до уровня осевых линий колесных пар.
– расстояние от равнодействующей давления ветра до уровня осевых линий колесных пар.
Из условия равновесия моментов, например относительно точки В, могут быть определены реакции опор от действия вертикальных сил, вызванных центробежной и ветровой нагрузками.

откуда
 , (5.10)
, (5.10)
Аналогично определяется рамная сила Н
 , (5.11)
, (5.11)
где  – коэффициент горизонтальной динамики
– коэффициент горизонтальной динамики
 , (5.12)
, (5.12)
где  , d – величины, зависящие от осности тележки и гибкости рессорного подвешивания;
, d – величины, зависящие от осности тележки и гибкости рессорного подвешивания;
F – коэффициент, равный для вагонов:
грузовых – 4,5
изотермических – 4
пассажирских – 3,5.
Поперечная составляющая сил трения, возникающая в месте контакта колеса с внутренним рельсом кривого участка
 , (5.13)
, (5.13)
где  – коэффициент трения при скольжении колеса по рельсу.
– коэффициент трения при скольжении колеса по рельсу.
 – вертикальная нагрузка, движущегося по внутреннему рельсу колеса.
– вертикальная нагрузка, движущегося по внутреннему рельсу колеса.
Боковое давление Н 1, приложенное к колесу, движущегося по наружному рельсу кривого участка пути, определяются из условия равновесия
 ,
,
откуда 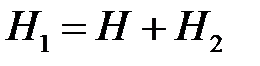 . (5.14)
. (5.14)
Вертикальная реакция рельсов от центробежной силы (схема в) определяется из условия равновесия моментов.
 ,
,
откуда  . (5.15)
. (5.15)
Вертикальные нагрузки от сил инерции необрессоренных масс определяют по 2-му закону Ньютона, как произведение массы элемента колесной пары на ускорение. При этом в качестве расчетного принимается наиболее неблагоприятное условие несимметричного действия инерционных сил. Например, на левом колесе оно возникает, а на правом – отсутствует. На основе обработки экспериментальных замеров ускорений установлена эмпирическая формула зависимости ускорения буксового узла от скорости движения вагона
 , (5.16)
, (5.16)
где D – величина, зависящая от типа вагона, определяемая по выше приведенной таблице.
 – сумма масс необрессоренных частей вагона, опирающихся на рельс:
– сумма масс необрессоренных частей вагона, опирающихся на рельс:
 , (5.17)
, (5.17)
где  ,
,  ,
,  – массы колесной пары, буксового узла и необрессоренных деталей, опирающихся на буксу.
– массы колесной пары, буксового узла и необрессоренных деталей, опирающихся на буксу.
Для расчетной схемы, приведенной на схеме г, может быть принят линейный закон изменения ускорения вдоль оси колесной пары. Если вертикальное ускорение левого колеса этой схемы 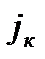 вычислять по формуле (5.16), то для ускорения средней части оси
вычислять по формуле (5.16), то для ускорения средней части оси  и правого буксового узла
и правого буксового узла  справедливы формулы
справедливы формулы
 , (5.18)
, (5.18)
 , (5.19)
, (5.19)
 . (5.20)
. (5.20)
Силы инерции, действующие на шейки оси (схема г):
– левую –  ; (5.21)
; (5.21)
– правую –  , (5.22)
, (5.22)
где  ,
,  – суммы необрессоренных масс, приходящихся на левую и правую шейки оси соответственно.
– суммы необрессоренных масс, приходящихся на левую и правую шейки оси соответственно.
Сила инерции левого колеса
 . (5.23)
. (5.23)
Средней части оси
 , (5.24)
, (5.24)
где  ,
,  – массы соответственно колеса и средней части оси. Сила
– массы соответственно колеса и средней части оси. Сила  приложена на расстоянии
приложена на расстоянии  от плоскости круга катания левого колеса.
от плоскости круга катания левого колеса.
Вертикальные реакции рельсов от действия инерционных сил определяются условиями равновесия

откуда
 . (5.25)
. (5.25)
Из условия  можно получить выражение
можно получить выражение
 (5.26)
(5.26)
Рассмотрение возможных комбинаций активных и реактивных нагрузок показывает, что при самом неблагоприятном сочетании сил к центрам шеек будут приложены вертикальные расчетные нагрузки (для схем а) – г)).
К левой:  ; (5.27)
; (5.27)
К правой:  . (5.28)
. (5.28)
Соответствующие вертикальные реакции рельсов определяются по формулам:
левого колеса:  (5.29)
(5.29)
правого колеса:  (5.30)
(5.30)
Поиск по сайту: