Денежный рынок. Классическая и кейнсианская теория спроса на деньги

Денежный рынок – это рынок, на котором продается и покупается особый товар – деньги. Основными его элементами являются спрос на деньги, предложение денег, цена денег (ставка ссудного процента). Роль денег выполняют не только наличные деньги, но и вклады до востребования, срочные вклады и т.п. Поэтому для расчета количества денег экономисты ввели понятие денежных агрегатов: М₁, М₂, М₃, М₄ (в порядке убывания степени ликвидности). Состав и количество используемых денежных агрегатов различаются по странам. Согласно классификации, используемой в США, денежные агрегаты представлены следующим образом:

M_l — наличные деньги вне банковской системы, депозиты до востребования, дорожные чеки, прочие чековые депозиты;

М₂ — агрегат M_l плюс нечековые сберегательные депозиты, срочные вклады (до 100 000 долл.), однодневные соглашения об обратном выкупе и др.;

М_З — агрегат М₂ плюс срочные вклады свыше 100 тыс. долл., срочные соглашения об обратном выкупе, депозитные сертификаты и др.;

М₄ — агрегат М₃ плюс казначейские сберегательные облигации, краткосрочные государственные обязательства, коммерческие бумаги и пр.

В макроэкономическом анализе чаще других используются агрегаты M_l и М₂. Иногда выделяется показатель наличности (МО или С от английского "currency") как часть M₁, а также показатель " квази-деньги " (QM) как разность между М₂ и M_l, т.е., главным образом, сберегательные и срочные депозиты, тогда M₂ = M₁ + QM.

Динамика денежных агрегатов зависит от многих причин, в том числе от движения процентной ставки. Так, при росте ставки процента агрегаты М₂, М_З могут опережать M_l, поскольку их составляющие приносят доход в виде процента. В последнее время появление в составе M_l новых видов вкладов, приносящих проценты, сглаживает различия в динамике агрегатов, обусловленные движением ставки процента.

Количественная теория денег определяет спрос на деньги с помощью уравнения обмена:

MV=PY,

где М — количество денег в обращении;

V — скорость обращения денег;

Р — уровень цен (индекс цен);

Y — объем выпуска (в реальном выражении).

Предполагается, что скорость обращения — величина постоянная, т.к. связана с достаточно устойчивой структурой сделок в экономике. Однако, с течением времени она может изменяться, например, в связи с внедрением новых технических средств в банковских учреждениях, ускоряющих систему расчетов. При постоянстве V уравнение обмена имеет вид:

При условии постоянства V изменение количества денег в обращении (М) должно вызвать пропорциональное изменение номинального ВНП (PY). Но, согласно классической теории, реальный ВНП (Y) изменяется медленно и только при изменении величины факторов производства и технологии. Можно предположить, что Y меняется с постоянной скоростью, а на коротких отрезках времени — постоянен. Поэтому колебания номинального ВНП будут отражать главным образом изменения уровня цен. Таким образом, изменение количества денег в обращении не окажет влияния на реальные величины, а отразится на колебаниях номинальных переменных. Это явление получило название " нейтральности денег ". Современные монетаристы, поддерживая концепцию "нейтральности денег" для описания долговременных связей между динамикой денежной массы и уровнем цен, признают влияние предложений денег на реальные величины в краткосрочном периоде (в пределах делового цикла).

Уравнение обмена может быть представлено в темповой записи (для небольших изменений входящих в него величин):

По правилу монетаристов, государство должно поддерживать темп роста денежной массы на уровне средних темпов роста реального ВНП, тогда уровень цен в экономике будет стабилен.

Приведенное уравнение обмена MV=PY связывают с именем американского экономиста И. Фишера. Используется и другая форма этого уравнения, так называемое кембриджское уравнение: M = kPY, где - величина, обратная скорости обращения денег. Коэффициент k, несет и собственную смысловую нагрузку, показывая долю номинальных денежных остатков (М) в доходе (PY). Строго говоря, величины V и k связаны с движением ставки процента, но в данном случае для простоты принимаются постоянными. Кембриджское уравнение предполагает наличие разных видов финансовых активов с разной доходностью (а не только наличность или M_l) и возможность выбора между ними при решении вопроса, в какой форме хранить доход.

Чтобы элиминировать влияние инфляции, обычно рассматривают реальный спрос на деньги, то есть

,

где величина — носит название " реальных запасов денежных средств ", или " реальных денежных остатков ".

Кейнсианская теория спроса на деньги — теория предпочтения ликвидности — выделяет три мотива, побуждающие людей хранить часть денег в виде наличности:

- трансакционный мотив (потребность в наличности для текущих сделок);

- мотив предосторожности (хранение определенной суммы наличности на случай непредвиденных обстоятельств в будущем);

- спекулятивный мотив (намерение приберечь некоторый резерв, чтобы с выгодой воспользоваться лучшим, по сравнению с рынком, знанием того, что принесет будущее).

Спекулятивный спрос на деньги основан на обратной зависимости между ставкой процента и курсом облигаций. Пусть Вы приобрели облигацию по курсу 100000 руб., приносящую фиксированный доход в 5000 руб. в год, что соответствует существующей на этот момент процентной ставке, равной 5%. Затем Вы решили продать эту облигацию. Но процентная ставка на рынке изменилась и равна уже 8%. За какую сумму Вы сможете теперь продать вашу облигацию при условии, что она приносит те же 5000 руб. дохода? По курсу 100 тыс. ее уже не купят, т.к. эти деньги могут принести 8000 руб. дохода при существующей рыночной ставке. Предполагая, что 5000 руб. соответствуют 8% дохода, получаем новый курс облигации, равный 62500 руб. Общая формула для определения текущего курса облигации такова: , где В – курс облигации в данный момент; а – фиксированная сумма дохода, которую приносит облигация; i – текущая рыночная ставка процента. В нашем примере . Кейнс для простоты предположил, что существует только две формы финансовых активов: наличность и облигации.

Если ставка процента растет, то цена облигации падает, спрос на облигации растет, что ведет к сокращению запаса наличных денег (меняется соотношение между наличностью и облигациями в портфеле активов), т.е. спрос на наличные деньги снижается. Таким образом, очевидна обратная зависимость между спросом на деньги и ставкой процента.

Обобщая два названных подхода — классический и кейнсианский — можно выделить следующие факторы спроса на деньги:

· уровень дохода;

· скорость обращения денег;

· ставка процента.

Классическая теория связывает спрос на деньги главным образом с реальным доходом. Кейнсианская теория спроса на деньги считает основным фактором ставку процента. Хранение денег в виде наличности связано с определенными издержками. Они равны проценту, который можно было бы получить, положив деньги в банк или использовав их на покупку других финансовых активов, приносящих доход. Чем выше ставка процента, тем больше мы теряем потенциального дохода, тем выше альтернативная стоимость хранения денег в виде наличности, а значит, тем ниже спрос на наличные деньги.

Оставляя в стороне наиболее сложный и противоречивый фактор — скорость обращения денег, по поводу которого отсутствует единство во взглядах среди экономистов, можно представить функцию спроса на реальные денежные остатки следующим образом:

,

где R – ставка процента; Y – реальный доход.

Из формулы видно, что фактором количественного спроса на деньги (М^D) выступает уровень цен. Если предположить, что связь между М^D и факторами спроса имеет линейную зависимость, то получим:

,

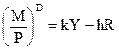где коэффициенты k и h отражают чувствительность спроса на деньги к доходу и ставке процента. Функция спроса на деньги показывает, что при любом данном уровне дохода величина спроса будет падать с ростом ставки процента и наоборот. Увеличение уровня дохода отразится сдвигом кривой спроса на деньги L^D вправо на величину kDY (рис. 6.1.).

Эмпирические данные подтверждают теоретическую модель спроса на деньги, обнаруживая, однако, наличие определенного временного лага между изменением факторов и реакцией спроса на деньги.

Различают номинальную и реальную ставки процента. Номинальная ставка - это ставка, назначаемая банками по кредитным операциям. Реальная ставка процента отражает реальную покупательную способность дохода, полученного в виде процента. Связь номинальной и реальной ставки процента описывается уравнением Фишера:

i = r + p,

где p – темп инфляции; i – номинальная ставка процента.

Уравнение показывает, что номинальная ставка процента может изменяться по двум причинам: из-за изменения реальной ставки и темпа инфляции.

Количественная теория и уравнение Фишера вместе дают связь объема денежной массы и номинальной ставки процента: рост денежной массы вызывает рост инфляции, а последняя приводит к увеличению номинальной ставки процента. Эту связь инфляции и номинальной ставки процента называют эффектом Фишера.

Отметим, что в долгосрочном периоде сохраняется отмеченная классиками "нейтральность денег", то есть изменение номинальной переменной (в данном случае p) может повлиять лишь на другую номинальную переменную (i), не затрагивая реальные величины (r). В краткосрочном периоде изменение номинальной величины может на какое-то время отразиться на реальной переменной. Так, при изменении темпов инфляции банки могут не сразу изменить назначаемую ими ставку процента (i), тогда, например, рост инфляции (p) снизит на некоторое время реальную ставку процента, что создаст благоприятные условия для инвесторов и других получателей кредитов. В этом случае r = i - p при высоких темпах инфляции используется более точная формула для определения реальной ставки процента:

Учитывая возросшее влияние на процессы в экономике инфляционных ожиданий экономических агентов, а также тот факт, что, устанавливая определенную ставку процента, банки имеют в виду ожидаемый в перспективе темп инфляции (p^е), поскольку фактическое его значение на данный момент не известно, формула Фишера несколько модифицируется:

i = r + p^e

На базе двух основных подходов к анализу спроса на деньги развивается множество современных денежных теорий, акцентирующих внимание на разных сторонах спроса на деньги. Так, в основе модели Баумоля-Тобнна лежит трансакционный спрос на деньги. С помощью этой модели можно определить, например, какую сумму в среднем за, период эко комический агент может хранить в виде наличности в зависимости от уровня своего дохода, альтернативной стоимости хранения денег в виде наличности (обычно ставки процента, i), издержек по переводу своих активов из одной формы в другую. Одновременно решается и вопрос о том, как часто следует переводить активы из одной формы в другую (см. Н.Г. Мэнкью Макроэкономика. Гл. 18).

Портфельный подход к спросу на деньги исходит из того, что наличность — лишь одна из составляющих портфеля финансовых активов экономических агентов. Решая вопрос об оптимальном количестве средств, которые можно держать в виде наличности, владелец портфеля исходит из того, какой доход могут обеспечить ему другие виды активов, и в то же время, насколько рискованно хранить средства в той или другой форме финансовых активов. Рост доходности акций и облигаций, например, будет снижать спрос на наличность. С другой стороны, рост риска потерять доход от неденежных форм активов увеличивает желание хранить деньги в виде наличности. Спрос на деньги ставится также в зависимость от общего богатства индивида, поскольку размеры этого богатства определяют объем портфеля активов в целом, а значит и всех его составляющих. Учитывается и влияние инфляции. Общая формула выглядит следующим образом:

,

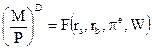где: r_s — предполагаемый реальный доход на акции,

r_b — предполагаемый реальный доход по облигациям,

p^e - ожидаемая инфляция, W — реальное богатство.

Причем только последний фактор положительно связан со спросом на деньги. Например, в случае высокой инфляции спрос на деньги уменьшается, экономические агенты стремятся перевести свои средства в реальные активы, не столь подверженные влиянию инфляции.

Очевидно, что данный подход к спросу на деньги имеет смысл прежде всего для агрегатов М₂, М₃ и более широких денег. Составляющие агрегата M_l практически не приносят дохода, но по степени риска почти аналогичны многим активам в правой части приведенной формулы (например, государственным облигациям). В этом случае утрачивается смысл сравнения правой и левой частей формулы: владельцам портфеля активов заведомо невыгодно держать средства в форме наличности или M_l, если можно поместить их в более прибыльные, но такие же по степени риска финансовые активы.

Эмпирическая оценка спроса на деньги может быть основана на имеющихся данных о существовавших в предшествующих периодах соотношениях между спросом на деньги и ВНП, ставкой процента, инфляцией. Однако в условиях переходной экономики при проведении структурной перестройки, финансовой реформы и пр., подобные оценки имеют ограниченное применение.

Другой подход может состоять в определении спроса на деньги на основе оценки вероятного изменения скорости обращения денег, ожидаемой инфляции и планируемого изменения объема реального ВНП (то есть исходя из уравнения MV=PY).

Поиск по сайту: