 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Завдання
|
Читайте также: |
Користуючись схемою Горнера, обрахувати значення вказаних многочленів при  і при
і при  . Виконати ділення даних многочленів на
. Виконати ділення даних многочленів на  і на
і на  .
.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 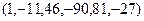
17. 
18. 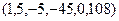
19. 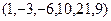
20. 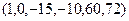
21. 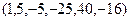
22. 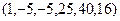
23. 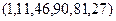
24. 
25. 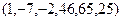
26. 
27. 
28. 
29. 
30. 
§ 2. Алгоритм Евкліда. Найбільший спільний дільник многочленів. Лінійне представлення найбільшого спільного дільника.
Має місце теорема про ділення з остачею.
Теорема:
 ст.
ст. 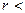 ст.
ст.  або
або 
Процес послідовного ділення многочлена  на многочлен
на многочлен  ,потім многочлена
,потім многочлена  на остачу, отриману при першому ділені, потім першу остачу на остачу, отриману при другому ділені і так далі називають алгоритмом Евкліда, який застосовувався до многочленів
на остачу, отриману при першому ділені, потім першу остачу на остачу, отриману при другому ділені і так далі називають алгоритмом Евкліда, який застосовувався до многочленів  і
і  .
.
Спільний дільник многочленів  і
і  , який ділиться на любий спільний дільник цих многочленів, називається їх найбільшим спільним дільником
, який ділиться на любий спільний дільник цих многочленів, називається їх найбільшим спільним дільником
(позначається  ).
).
При застосуванні алгоритму Евкліда до многочленів  і
і  ,останній, відмінний від нуля, залишок стає рівним найбільшому спільному дільнику цих многочленів.
,останній, відмінний від нуля, залишок стає рівним найбільшому спільному дільнику цих многочленів.
Найбільший спільний дільник многочленів можна лінійно представити через дані многочлени:

Поиск по сайту: