 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Завдання. Розкласти дані многочлени на незвідні многочлени над полем комплексних чисел і над полем дійсних чисел
|
Читайте также: |
Розкласти дані многочлени на незвідні многочлени над полем комплексних чисел і над полем дійсних чисел.
1.  16.
16. 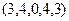
2.  17.
17. 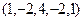
3.  18.
18. 
4.  19.
19. 
5.  20.
20. 
6.  21.
21. 
7.  22.
22. 
8.  23.
23. 
9.  24.
24. 
10.  25.
25. 
11. 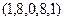 26.
26. 
12.  27.
27. 
13.  28.
28. 
14.  29.
29. 
15  30.
30. 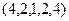 .
.
§ 4. Похідна многочлена. Розкладання многочлена
за степенями 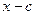 .
.
При діленні многочлена 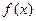 , степені
, степені  , із кільця многочленів над полем характеристики нуль на
, із кільця многочленів над полем характеристики нуль на 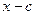 , потім першої неповної частки на
, потім першої неповної частки на 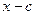 , потім другої неповної частки на
, потім другої неповної частки на 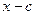 і так далі остача від ділення відповідно дорівнює
і так далі остача від ділення відповідно дорівнює  Таким чином, користуючись схемою Горнера, можна визначити значення похідних многочлена і розкласти многочлен за степенями
Таким чином, користуючись схемою Горнера, можна визначити значення похідних многочлена і розкласти многочлен за степенями 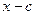 за формулою Тейлора, яка має вигляд:
за формулою Тейлора, яка має вигляд:  .
.
Поиск по сайту: