 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача Д1
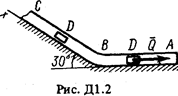
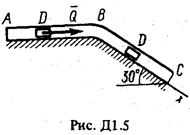
Груз D массой т, получив в точке А начальную скорость u 0, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные,или один горизонтальный, а другой наклонный (рис. Д1.0-Д1.9, табл. Д1). На участке АВ на груз кроме силы тяжести действуют постоянная сила  (ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости
(ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости  груза (направлена против движения).
груза (направлена против движения).

| 
|
| 
|

| 
|

| 
|

| 
|
Таблица Д1
| Номер условия | m, кг | u0, м/с | Q, H | R, H | l, м | t 1, с | Fx,H |
| 2,4 | 0,8 u 2 | 1,5 | - | 4sin(4 t) | |||
| 0,4 u | - | 2,5 | -5 cos(4 t) | ||||
| 0,5 u 2 | - | 6t2 | |||||
| 1,8 | 0,3 u | - | -2 cos(2 t) | ||||
| 0,6 u 2 | - | -5sin(2 t) | |||||
| 4,5 | 0,5 u | - | 3 t | ||||
| 0,8 u 2 | 2,5 | - | 6 cos(4 t) | ||||
| 1,6 | 0,4 u | - | -3sin(4 t) | ||||
| 4,8 | 0,2 u 2 | - | 4 cos(2 t) | ||||
| 0,5 u | - | 4sin(2 t) |
В точке В груз, не изменяя значения своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует переменная сила  , проекция которой Fx на ось х задана в таблице.
, проекция которой Fx на ось х задана в таблице.
Считая груз материальной точкой и зная расстояние АВ = l или время t 1 движения груза от точки А до точки В, найти закон движения груза на участке ВС, т.е. x=f(t), где х = BD. Трением груза о трубу пренебречь.
Указания. Задача Д1 - на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке АВ, учтя начальные условия. Затем, зная время движения на участке АВ или его длину, определить, какую скорость будет иметь груз в точке В. Эта скорость будет начальной для движения груза на участке ВС. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отсчет врем
ени от момента, когда груз находится в точке В, и полагая, что в этот момент времени t = 0. При интегрировании уравнения движения на участке АВ в случае, когда задана длина l участка, целесообразно перейти в уравнении к переменному х, учтя, что

Пример Д1. На вертикальном участке АВ трубы (рис. Д1) на груз D массой т действуют сила тяжести и сила сопротивления  ; расстояние от точки А, где u = u 0, до точки В равно l. На наклонном участке ВС на груз действуют сила тяжести и переменная сила F = F (t), заданная в ньютонах.
; расстояние от точки А, где u = u 0, до точки В равно l. На наклонном участке ВС на груз действуют сила тяжести и переменная сила F = F (t), заданная в ньютонах.

| Дано: т = 2 кг, R = mu 2, где m = 0,4 кг/м, u 0 = 5 м/с, l = 2,5 м, fх = 16 sin (4 t). Определить: х = f (t) - закон движения груза на участке ВС. |
Решение. 1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы  Проводим ось Az и составляем дифференциальное уравнение движения груза в проекции на эту ось:
Проводим ось Az и составляем дифференциальное уравнение движения груза в проекции на эту ось:
 (1)
(1)
Далее находим: Рz = Р = mg, Rz = -R = - mu 2; подчеркиваем, Что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что uz = u, получим
 (2)
(2)
Введем для сокращения записей обозначения
 (3)
(3)
где при подсчете принято g» 10 м/с2. Тогда уравнение (2) можно представить в виде
 (4)
(4)
Разделяя в уравнении (4) переменные, а затем беря от обеих частей интегралы, получим
 (5)
(5)
По начальным условиям при z = 0 u = u 0, что дает С 1 =  , и из равенства (5) находим
, и из равенства (5) находим


 (6)
(6)
Полагая в равенстве (6) z = l = 2,5 м и заменяя k и п их значениями (3), определим скорость u B груза в точке В (u0 = 5 м/с, число е = 2,7):
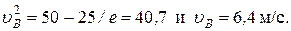 (7)
(7)
2. Теперь рассмотрим движение груза на участке ВС; найденная скорость u B будет для движения на этом участке начальной скоростью (u 0 = u B). Изображаем груз (в произвольном положении) и действующие на него силы 
Проведем из точки В ось Вх и составим дифференциальное уравнение движения груза в проекции на эту ось:
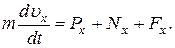 (8)
(8)
Так как Рх = Р sin 30° = 0,5 mg, Nx = 0, Fx = 16 sin (4 t), то уравнение (8) примет вид
 (9)
(9)
Разделив обе части равенства на т = 2 кг и полагая опять g» 10 м/с2, получим
 (10)
(10)
Умножая обе части уравнения (10) на dt и интегрируя, найдем
 (11)
(11)
Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t = 0. Тогда при t = 0 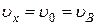 , где u B дается равенством (7). Подставляя эти величины в (11), получим
, где u B дается равенством (7). Подставляя эти величины в (11), получим
C 2 = u B + 2 cos 0 = 6,4 + 2 = 8,4.
При найденном значении C 2, уравнение (11) дает
 (12)
(12)
Умножая здесь обе части на dt и снова интегрируя, найдем
 (13)
(13)
Так как при t = 0 х = 0, то С 3 = 0, и искомый закон движения груза будет
х = 2,5 t 2 + 8,4 t - 0,5 sin (4 t), (14)
где х - в метрах, t - в секундах.
Задача Д3
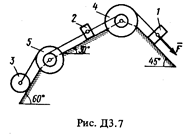
Механическая система состоит из грузов 1 и 2 (коэффициент трения грузов о плоскость f = 0,1), цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R 4 = 0,3 м, r 4 = 0,1 м, R 5 = 0,2 м, r 5 = 0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу) (рис. Д3.0 – Д3.9, табл. Д3). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям.

| 
|

| 
|

| 
|

| 
|

| 
|
Под действием силы F = f (s), зависящей от перемещения точки приложения силы, система приходит в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивлений, равные соответственно M 4 и М 5.
Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы 
 равно s,. Искомая величина указана в столбце "Найти" таблицы, где обозначено:
равно s,. Искомая величина указана в столбце "Найти" таблицы, где обозначено: 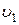 - скорость груза 1,
- скорость груза 1,  - скорость центра масс катка 3,
- скорость центра масс катка 3, 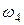 - угловая скорость тела 4 и т.д.
- угловая скорость тела 4 и т.д.
Таблица Д3
| Номер усло-вия | m 1, кг | m2, кг | m 3, кг | m 4, кг | m 5, кг | M 4, Н×м | M 5, Н×м | F = f(s) | s 1, м | Найти |
| 0,8 | 50(2+3 s) | 1,0 | 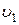
| |||||||
| 0,6 | 20(5+2 s) | 1,2 | 
| |||||||
| 0,4 | 80(3+4 s) | 0,8 | 
| |||||||
| 0,3 | 40(4+5 s) | 0,6 | 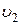
| |||||||
| 0,6 | 30(3+2 s) | 1,4 | 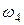
| |||||||
| 0,9 | 40(3+5 s) | 1,6 | 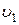
| |||||||
| 0,8 | 60(2+5 s) | 1,0 | 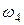
| |||||||
| 0,6 | 30(8+3 s) | 0,8 | 
| |||||||
| 0,3 | 40(2+5 s) | 1,6 | 
| |||||||
| 0,4 | 50(3+2 s) | 1,4 | 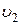
|
Указания. Задача ДЗ - на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел: эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении кинетической энергии катка, совершающего плоское движение, для установления зависимости между его угловой скоростью и скоростью его центра масс воспользоваться понятием о мгновенном центре скоростей (кинематика). При определении работы все перемещения следует выразить через заданное перемещение s 1, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
Когда по данным таблицы m 2 = 0, груз 2 на чертеже не изображать; шкивы 4 и 5 всегда входят в систему.
Пример ДЗ. Механическая система (рис. ДЗ) состоит из сплошного цилиндрического катка l, ступенчатого шкива 2 с радиусами ступеней R 2 и r 2 (масса шкива равномерно распределена по его внешнему ободу) и груза 3 (коэффициент трения груза о плоскость равен f). Тела системы соединены друг с другом нитями, намотанными на шкив 2.

| Под действием силы F = f (s), зависящей от перемещения s точки ее приложения, система приходит в движения из состояния покоя. При движении на шкив 2 действует постоянный момент М 2 сил сопротивления.
Дано: m 1 = 4 кг, m 2 = 10кг,
m 3 = 8 кг, R 2 = 0,2 м, r 2 = 0,1м, f = 0,2. М 2 = 0,6 Н × м, F = 2(1+2 s) Н, s 1 = 2м.
Определить: скорость  центра масс катка, когда s = s 1.
центра масс катка, когда s = s 1.
|
Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из тел 1 2, 3, соединенных нитями. Изобразим все действующие на систему внешние силы: активные 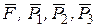 , момент сопротивления М 2 реакции
, момент сопротивления М 2 реакции  и силы трения
и силы трения  и
и  .
.
Для определения  воспользуемся теоремой об изменении кинетической энергии системы
воспользуемся теоремой об изменении кинетической энергии системы
 (1)
(1)
2. Определяем Т 0 и Т. Так как в начальный момент система находилась в покое, то Т 0 = 0. Величина Т равна сумме энергий всех тел системы:
 (2)
(2)
Учитывая, что тело 1 совершает плоское движение, тело 3 движется поступательно, а тело 2 вращается вокруг неподвижной оси, получим
 (3)
(3)
Все входящие сюда скорости следует выразить через искомую  . Приняв во внимание, что точка K 1 - мгновенный центр скоростей катка 1, и обозначив радиус катка через r 1, получим
. Приняв во внимание, что точка K 1 - мгновенный центр скоростей катка 1, и обозначив радиус катка через r 1, получим
 (4)
(4)
Кроме того, входящие в (3) моменты инерции имеют значения
 (5)
(5)
Подставив все величины (4) и (5) в равенство (3), а затем используя равенство (2) получим окончательно:
 (6)
(6)
3. Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда точка С 1 пройдет путь s 1. Одновременно все перемещения следует выразить через заданную величину s 1, для чего учтем, что здесь зависимость между перемещениями будет такой же, как и между соответствующими скоростями в равенствах (4), т.е. 
 . В результате получим:
. В результате получим:

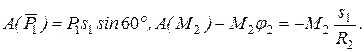


Работа остальных сил равна нулю, так как точка K 1, где приложены силы  и
и  , является мгновенным центром скоростей, точка O, где приложены
, является мгновенным центром скоростей, точка O, где приложены  , и
, и  , неподвижна, а реакция
, неподвижна, а реакция  перпендикулярна перемещению груза 3. Тогда окончательно
перпендикулярна перемещению груза 3. Тогда окончательно
 (7)
(7)
4. Подставив выражения (6) и (7) в уравнение (1) и учитывая, что T 0 = 0, получим

 (8)
(8)
При числовых значениях заданных величин равенство (8) дает

Отсюда находим искомую скорость.
Ответ:  = 1.53м/с.
= 1.53м/с.
Задача Д4
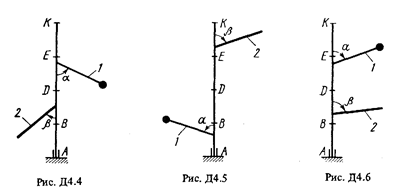
Вертикальный вал АК (рис. Д4.0-Д4.9, табл. Д4), вращающийся с постоянной угловой скоростью w = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д4 в столбце 2 (АВ = ВО = DE = EК = b). К валу жестко прикреплены невесомый стержень 1 длиной l 1 = 0,4 м с точечной массой m 1 = 6 кг на конце и однородный стержень 2 длиной l 2 = 0,6 м, имеющий массу m 2 = 4 кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы a и b - в столбцах 5 и 6. Пренебрегая весом вала, определить реакции подпятника и подшипника. При окончательных подсчетах принять b = 0,4 м.

|
|

|
Таблица Д4
| Номер условия | Подшипник в точке | Крепление | a° | b° | Номер условия | Подшипник в точке | Крепление | a° | b° | ||
| стержня 1 в точке в точке | стержня 2 в точке в точке | стержня 1 в точке | стержня 2 в точке | ||||||||
| В | D | K | D | K | B | ||||||
| D | D | E | E | B | K | ||||||
| E | D | B | K | E | B | ||||||
| K | D | E | D | E | K | ||||||
| B | E | D | E | K | D |
Указания. Задача Д4 - на применение к изучению движения системы принципа Даламбера. При решении задачи учесть, что когда силы инерции частиц тела (в данной задаче стержня 2) имеют равнодействующую  , то численно
, то численно  = ma C, где а C - ускорение центра масс С стержня, но линия действия силы
= ma C, где а C - ускорение центра масс С стержня, но линия действия силы  в общем случае не проходит через точку С (см. пример Д4).
в общем случае не проходит через точку С (см. пример Д4).

| Пример Д4. С невесомым валом АВ, вращающимся с постоянной угловой скоростью w, жестко скреплен стержень OD длиной l и массой m 1, имеющий на конце груз массой m 2 (рис.Д4). Дано: b 1 = 0,6 м, b 2 = 0,2 м, a = 30°, l = 0,5 м, m 1 = 3 кг, m 2 = 2 кг, w = 6 с-1. Определить: реакции подпятника А и подшипника В. |
Решение. Для определения искомых реакций рассмотрим движение механической системы, состоящейиз вала АВ, стержня OD и груза, и применим принцип Даламбера. Проведем вращающиеся вместе с валомоси Аху так, чтобы стержень лежал в плоскости ху, и изобразим действующие на систему внешние силы: силы тяжести  , составляющие
, составляющие  реакции подпятника и реакцию
реакции подпятника и реакцию  подшипника.
подшипника.
Согласно принципу Даламбера присоединим к этим силам силы инерции элементов стержня и груза, считая груз материальной точкой. Так как вал вращается равномерно (w = const), то элементы стержня имеют только нормальные ускорения  направленные к оси вращения, а численно
направленные к оси вращения, а численно  , где hk - расстояние элемента от оси. Тогда силы инерции
, где hk - расстояние элемента от оси. Тогда силы инерции  будут направлены от оси вращении и численно
будут направлены от оси вращении и численно  , где D m - масса элемента. Поскольку все
, где D m - масса элемента. Поскольку все  пропорциональны hk, то эпюра этих параллельных сил образует треугольник и их можно заменить равнодействующей
пропорциональны hk, то эпюра этих параллельных сил образует треугольник и их можно заменить равнодействующей  , линия действия которой проходит через центр, тяжести этого треугольника, т.е. на расстоянии H 1 от вершины О, где
, линия действия которой проходит через центр, тяжести этого треугольника, т.е. на расстоянии H 1 от вершины О, где 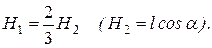
Но, как известно, равнодействующая любой системы сил равна ее главному вектору, а численно главный вектор сил инерции стержня  = m 1 a C, где а C ускорение центра масс стержня; при этом, как и для любого элемента стержня, а C = а Cn = w 2 h C = w 2 OC sin a (OC= l/ 2). В результате получим
= m 1 a C, где а C ускорение центра масс стержня; при этом, как и для любого элемента стержня, а C = а Cn = w 2 h C = w 2 OC sin a (OC= l/ 2). В результате получим

Аналогично для силы инерции  груза найдем, что она тоже направлена от оси вращения, а численно
груза найдем, что она тоже направлена от оси вращения, а численно 
Так как все действующие силы и силы инерции лежат в плоскости ху, то и реакции подпятника А и подшипника В тоже лежат в этой плоскости, что было учтено приих изображении.
По принципу Даламбера, приложенные внешние силы и силы инерции образуют уравновешенную систему сил. Составляя для этой плоской системы сил три уравнения равновесия, получим:
 (1)
(1)
 (2)
(2)
 (3)
(3)
Подставив сюда числовые значения всех заданных и вычисленных величин и решив эту систему уравнений, найдем искомые реакции.
Ответ: XA =-11,8 Н, YA =49,1 Н, XB =-19,7 Н.
Знаки указывают, что силы  и
и  направлены противоположно показанным на рис. Д4.
направлены противоположно показанным на рис. Д4.
6. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Поиск по сайту: