АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Контрольные работы

Читайте также:
  1. I. КУРСОВЫЕ РАБОТЫ
  2. I. ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ
  3. II. ДИПЛОМНЫЕ РАБОТЫ
  4. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  5. II. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КУРСОВОЙ РАБОТЫ
  6. III. Задания для самостоятельной работы по изучаемой теме.
  7. III. Задания для самостоятельной работы по изучаемой теме.
  8. III. Задания для самостоятельной работы по изучаемой теме.
  9. III. Задания для самостоятельной работы по изучаемой теме.
  10. III. Задания для самостоятельной работы по изучаемой теме.
  11. III. Задания для самостоятельной работы по изучаемой теме.
  12. III. Требования охраны труда во время работы

Задача 1. Трехступенчатый брус жестко закрепленный одним концом загружен сосредоточенными силами F1, F2 и собственным весом (рис.1). Требуется: 1) написать аналитические выражения нормальных сил (N), нормальных напряжений (σ) и абсолютных удлинений (∆l) для каждого силового участка; 2) определить значения N и σ для характерных сечений и ∆l для силовых участков; 3) определить перемещения границ силовых участков (δ); 4) построить эпюры N, σ, δ. Данные взять из табл.2. Принять Е = 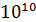Па.

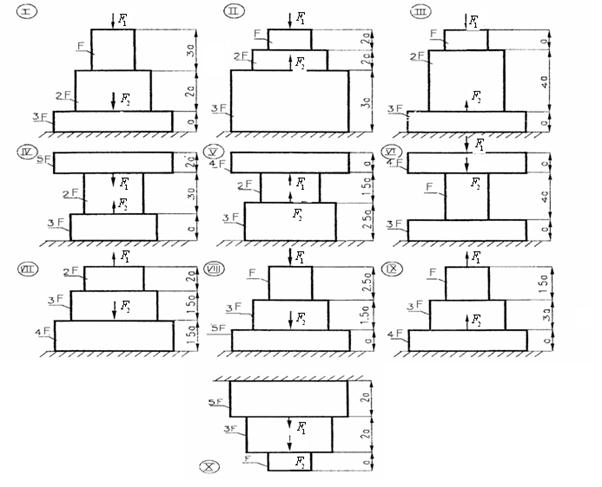
Рисунок 1 – Схемы брусьев

Таблица 2

№ строки Схема по рис.1 A, см2 a, м F1, кН F2, кН γ, кН/м3
  I.   1,5      
  II.   1,6      
  III.   1,7      
  IV.   1,8      
  V.   1,9      
  VI.   2,0      
  VII.   2,0      
  VIII.   2,1      
  IX.   2,2      
  X.   2,3      
  е г д е д г

Задача 2. Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням с помощью шарниров (рис. 2). Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу Q; 2) найти допускаемую нагрузку Qдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [ ] = 160 МПа; 3) найти предельную грузоподъемность системы Qyк и допускаемую нагрузку Qдоп, если предел текучести y = 240 МПа и запас прочности k= l,5; 4) сравнить величины Qдоп, полученные при расчете по допускаемым напряжениям (см. п. 2) и допускаемым нагрузкам (см.п.3).Данные взять из табл. 3

Рисунок 2 – Расчётные схемы

Таблица 3

№ строки Схема по рис.2 А, см2 a м b м c м
  I.   2.0 2.0 1.2
  II.   1.6 2.1 1.3
  III.   1.4 2.2 1.4
  IV.   1.8 2.3 1.5
  V.   1.9 2.4 1.6
  VI.   2.0 2.5 1.7
  VII.   1.2 2.6 1.8
  VIII.   1.3 2.7 1.9
  IX.   1.5 2.8 2.0
  X.   1.1 2.9 2.1
  е д г д е

Указания. Для определения двух неизвестных усилий в стержнях следует составить одно уравнение статики и одно уравнение деформаций.

Для ответа на третий вопрос задачи следует иметь в виду, что в одном из стержней напряжение больше, чем в другом; условно назовем этот стержень первым. При увеличении нагрузки напряжение в первом стержне достигнет предела текучести раньше, чем во втором. Когда это произойдет, напряжение в первом стержне не будет некоторое время расти даже при увеличении нагрузки, система станет как бы статически определимой, нагруженной силой Q (пока еще неизвестной) и усилием в первом стержне:

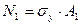. (1)

При дальнейшем увеличении нагрузки напряжение и во втором стержне достигнет предела текучести:

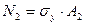. (2)

Написав уравнение статики и подставив в него значения усилий (1) и (2), найдем из этого уравнения предельную грузоподъемность Qку.

Задача 3. К стальному валу приложены три известных момента: М1, M2, M3 (рис. 3).

Требуется:1) установить, при каком значении момента X угол поворота правого концевого сечения вала равен нулю; 2) построить эпюру крутящих моментов; 3)при заданном значении Rср определить диаметр вала из расчета на прочность и округлить его до ближайшей большей величины, соответственно равной 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм; 4) построить эпюру углов закручивания; 5) найти наибольший относительный угол закручивания (на 1 м длины). Данные взять из табл. 4.

Таблица 4

№ строки Схема по рис.3 Расстояние, м   Моменты, кНм Rср, МПа
a b c M1 M2 M3
  I. 1.0 2.0 1.2 1.0 2.0 1.2  
  II. 1.1 2.1 1.3 1.1 2.1 1.1  
  III. 1.2 2.3 1.4 1.2 2.3 1.4  
  IV. 1.3 2.4 1.5 1.3 2.4 1.5  
  V. 1.4 2.5 1.6 1.4 2.5 1.6  
  VI. 1.5 2.6 1.7 1.5 2.6 1.7  
  VII. 1.6 2.7 1.8 1.6 2.7 1.8  
  VIII. 1.7 2.8 1.9 1.7 2.8 1.9  
  IX. 1.8 2.9 2.0 1.8 2.9 2.0  
  X. 1.9 3.0 2.2 1.9 3.0 2.2  
  е г д е г д е е

 

Рисунок 3 – Схемы стальных валов

Задача 4. Для заданного в табл. 5 поперечного сечения, состоящего из двутавра, равнобокого уголка и швеллера (рис. 4), требуется: 1) определить положение центра тяжести; 2) найти осевые (экваториальные) и центробежный моменты инерции относительно случайных осей, проходящих через центр тяжести (Xc и Yc ); 3) определить направление главных центральных осей (и и n); 4) найти моменты инерции относительно главных центральных осей; 5) вычертить сечение в масштабе 1:2 и указать на нем все размеры в числах и все оси.

При расчете все необходимые данные следует брать из таблиц сортамента и ни в коем случае не заменять части профилей прямоугольниками.

Таблица 5

№ строки Тип сечения по рис.4 Швеллер Равнобокий уголок Двутавр
  I.   80 X 80 X 6  
  II. 24а 80 X 80 X 7 18а
  III.   90 X 90 X 7 20а
  IV. 18а 90 X 90 X 9 22а
  V. 20а 90 X 90 X 6 24а
  VI. 18а 100 X 100 X 7 27а
  VII.   100 X 100 X 8  
  VIII.   100 X 100 X 14 30а
  IX.   125 X 125 X 16  
  X.   80 X 80 X 8  
 

е г д е

 

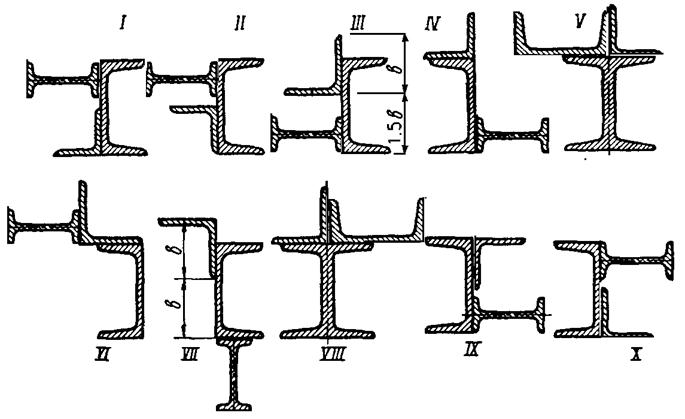
Рисунок 4 – Схемы поперечных сечений

Задача 5. Для заданных двух схем балок (рис. 5) требуется написать выражения Qи М для каждого участка в общем виде, построить эпюры Q и М, найти Мmax и подобрать: а) для схемы а деревянную балку круглого поперечного сечения при R = 10 МПа; б) для схемы б — стальную балку двутаврового поперечного сечения при R = 200 МПа. Данные взять из табл. 6.

 

Таблица 6

№ строки Схема по рис.5 l1 l2 Расстояние в долях пролета М, кН∙м Сосредоточенная сила F, кН q, кН/м
м a1/a a2/a a3/a
  I. 2.0 4.4            
  II. 1.9 5.6            
  III. 1.8 6.8            
  IV. 1.7 7.2            
  V. 1.6 4.0            
  VI. 1.5 4.8            
  VII. 1.6 5.8            
  VIII. 1.8 6.2            
  IX. 1.7 6.8            
  X. 2.0 7.0            
  е д е г д е г д е
                     

 

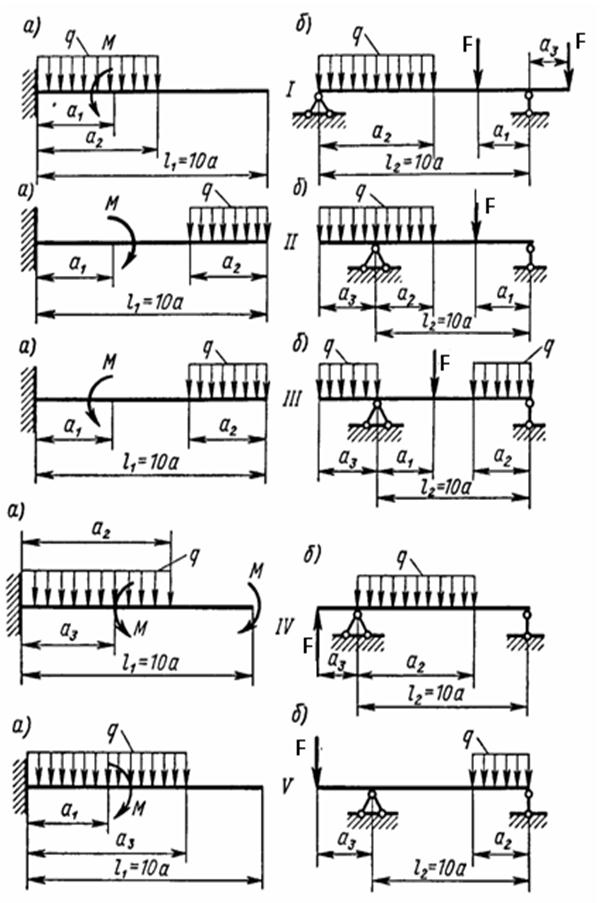
Рисунок 5 – Схемы балок

Рисунок 5 – Схемы балок (продолжение)

 
 


Задача 6. Определить прогиб свободного конца балки переменного сечения (рис. 6). Данные взять из табл. 7.

Указания. Проще всего задачу можно решить графоаналитическим методом, построив эпюру M/EJ и приняв ее за фиктивную нагрузку. Левый конец фиктивной балки должен быть свободен, а правый – защемлен.

Рисунок 6 – Схемы балок переменного сечения

Таблица 7

№ строки Схема по рис.6 a b k
  I. 0,1 0,1 1,5
  II. 0,2 0,2  
  III. 0,3 0,3  
  IV. 0,4 0,4  
  V. 0,5 0,5  
  VI. 0,6 0,6  
  VII. 0,7 0,7  
  VIII. 0,8 0,8  
  IX. 0,9 0,9  
  X. 1,0 1,0  
  е г е д

Задача 7. Для балки, изображенной на рис. 7, требуется: 1) найти изгибающий момент на левой опоре (в долях ql2); 2) построить эпюры Q и М; 3)построить эпюру прогибов, вычислив три ординаты в пролете и две – на консоли. Данные взять из табл.7

Указания. Для ответа на первый вопрос нужно выбрать основную систему в виде свободно лежащей на двух опорах балки и составить уравнение деформаций, выражающее мысль, что суммарный угол поворота на левой опоре от заданной нагрузки и от опорного момента равен нулю.

Можно также решить задачу иначе, составив два уравнения: 1) уравнение статики в виде суммы моментов всех сил относительно правой опоры; 2) уравнение метода начальных параметров, выражающее мысль, что прогиб на правой опоре равен нулю. Из этих двух уравнений можно найти изгибающий момент и реакцию на левой опоре.

Для ответа на третий вопрос целесообразнее использовать метод начальных параметров, так как два начальных параметра (у0 и q0) известны.

При построении эпюры прогибов надо учесть, что упругая линия балки обращена выпуклостью вниз там, где изгибающий момент положительный, и выпуклостью вверх там, где он отрицательный. Нулевым точкам эпюры М соответствуют точки перегиба упругой линии.

Рисунок 7 – Схемы балок

 

Задача 8. Короткая бетонная колонна, поперечное сечение которого изображено на рис. 8, сжимается продольной силой F, приложенной в точке А. Требуется:1) вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив эти напряжения через F и размеры сечения; 2) найти допускаемую нагрузку F при заданных размерах сечения и расчётных сопротивлениях для материала на сжатие Rc и на растяжение Rp. Данные взять из табл. 8.

 
 

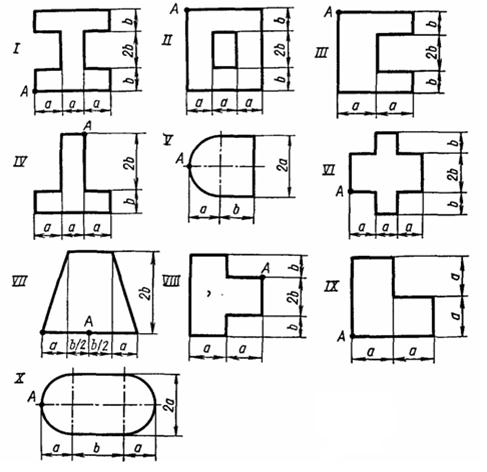
Рисунок 8 – Схемы колонн

Таблица 8

№ строки Схема по рис.8 a b Rс Rр
см МПа
  I.       4,0
  II.       3,5
  III.       3,0
  IV.       3,2
  V.       2,5
  VI.       2,0
  VII.       3,5
  VIII.       4,0
  IX.       3,2
  X.       2,5
  е г д е д

Задача 9. На рис. 9 изображена в аксонометрии ось ломаного стержня круглого поперечного сечения, расположенная в горизонтальной плоскости, с прямыми углами в точках A и В. На стержень действует вертикальная нагрузка. Требуется: 1) построить отдельно (в аксонометрии) эпюры изгибающих и крутящих моментов; 2) установить опасное сечение и найти для него расчетный момент по четвертой теории прочности. Данные взять из табл. 9.


Рисунок 9 – Схемы ломаных стержней

Таблица 9

№ строки Схема по рис.9 a
  I. 0.6
  II. 0.7
  III. 0.8
  IV. 0.9
  V. 1.0
  VI. 1,1
  VII. 1,2
  VIII. 1,3
  IX. 1,4
  X. 1,5
  е д

Задача 10. Стальная стойка длиной l сжимается силой F. Требуется: 1) найти размеры поперечного сечения при расчётном сопротивлении на простое сжатие R = 200 МПа (расчет производить последовательными приближениями, предварительно задавшись коэффициентом j=0,5); 2) найти значение критической силы и коэффициент запаса устойчивости. Данные взять из табл. 10.

Задача 11. На двутавровую балку, свободно лежащую на двух жестких опорах (рис. 10), с высоты h падает груз Q. Требуется: 1) найти наибольшее нормальное напряжение в балке; 2) решить аналогичную задачу при условии, что правая опора заменена пружиной, податливость которой (т. е. осадка от груза 1 кН) равна a; 3) сравнить полученные результаты. Данные взять из табл. 11

Указание: При наличии упомянутой в п. 2 пружины Dст=Dб+bDпр, где Dб—прогиб балки, лежащей на жестких опорах, в том сечении, где приложена сила Q (при статическом действии этой силы); Dпр — осадка пружины от реакции, возникающей от силы Q; b — коэффициент, устанавливающий зависимость между осадкой пружины и перемещением точки приложения силы Q, вызванным поворотом всей балки вокруг центра шарнира левой опоры как жесткого целого(коэффициент b находят из подобия треугольников).

Рисунок 10 – Схемы балок

 
 
 


Таблица 11

№ строки Схема по рис.10 № двутавра l, м Q, Н h, см 103 a, м/кН
  I.   2,1      
  II. 20а 2,2      
  III.   2,3      
  IV. 24а 2,4      
  V.   2,5      
  VI. 27а 2,6      
  VII.   2,7      
  VIII. 30а 2,8      
  IX.   2,9      
  X.   3,0      
  е д е г д е

 

 


Учебное издание

 

 

Составители: Соловей Павел Иванович

 

Хвисевич Виталий Михайлович

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.012 сек.)